Обобщенные силы

Рис.71

Рис.70

Рис.69

Положение точек кривошипно-шатунного механизма (рис.70) можно определить заданием угла поворота 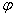кривошипа или расстоянием s, определяющим положение ползуна В (при ).

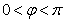Положение сферического маятника (рис.71) определяется заданием двух параметров, углов 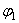и .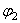

Минимальное количество независимых друг от друга обобщенных координат, которых достаточно, чтобы полностью и однозначно определить положение всех точек системы, называют числом степеней свободы этой системы.

Вообще для любой материальной системы можно назначить несколько обобщенных координат. Например, у кривошипно-шатунного механизма (рис.70) указаны две обобщенные координаты и 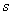. Но это не значит, что у механизма две степени свободы, так как одну координату можно определить через другую:

.

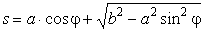А вот у маятника (рис.71) две степени свободы, т.к. определяется его положение двумя независимыми обобщенными координатами. Кстати, если длина маятника изменяется, то для определения положения точки М потребуется еще один параметр – обобщенная координата l, длина нити. И у маятника станут три степени свободы.

Обобщенные координаты в общем случае будем обозначать буквой q.

Пусть материальная система имеет s степеней свободы. Положение ее определяется обобщенными координатами: q ₁, q ₂, q ₃,…, q_k,…, q_{s. .}

Нетрудно убедиться, что декартовы координаты n точек системы можно определить как функции обобщенных координат и времени:

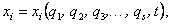
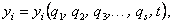(5)

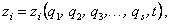
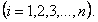
Так у маятника (рис.71) координаты точки М

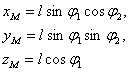
есть функции координат l, 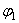и 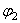, и времени t, если l = l(t).

Соответственно, и радиус-вектор точек системы можно определить как функцию обобщенных координат и времени:

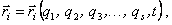
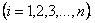(6)

Каждой обобщенной координате 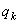можно вычислить соответствующую ей обобщенную силу Q_k.

Вычисление производится по такому правилу.

Чтобы определить обобщенную силу Q_k, соответствующую обобщенной координате q_k, надо дать этой координате приращение 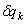(увеличить координату на эту величину), оставив все другие координаты неизменными, вычислить сумму работ всех сил, приложенных к системе, на соответствующих перемещениях точек и поделить ее на приращение координаты :

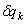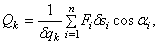(7)

где – 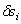перемещение i -той точки системы, полученное за счет изменения k –той обобщенной координаты.

Обобщенная сила определяется с помощью элементарных работ. Поэтому эту силу можно вычислить иначе:

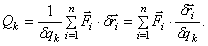
И так как 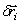есть приращение радиуса-вектора 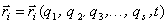за счет приращения координаты 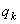при остальных неизменных координатах и времени t, отношение 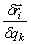можно определять как частную производную 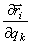. Тогда

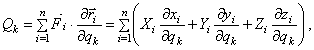(8)

где координаты точек – функции обобщенных координат (5).

Если система консервативная, то есть движение происходит под действием сил потенциального поля, проекции которых 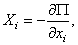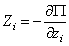, где 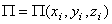, а координаты точек – функции обобщенных координат, то

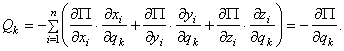(9)

Обобщенная сила консервативной системы есть частная производная от потенциальной энергии по соответствующей обобщенной координате со знаком минус.

Конечно, при вычислении этой обобщенной силы потенциальную энергию следует определять как функцию обобщенных координат

П = П(q ₁, q ₂, q ₃,…, q_s).

Замечания.

Первое. При вычислении обобщенных сил реакции идеальных связей не учитываются.

Второе. Размерность обобщенной силы зависит от размерности обобщенной координаты. Так если размерность [ q ] – метр, то размерность

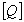= Нм/м = Ньютон, если [ q ] – радиан, то 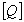= Нм; если [ q ] = м², то 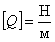и т.п.

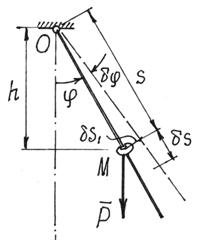
Пример 23. По качающемуся в вертикальной плоскости стержню скользит колечко М весом Р (рис.72). Стержень считаем невесомым. Определим обобщенные силы.