2017-12-16
967
Методика приведения масс основана на равенстве кинетических энергий исходного машинного агрегата и заменяющей его динамической модели. Запишем для них уравнение изменения кинетической энергии.
Кинетическая энергия:
| Движение твердого тела | Кинетическая энергия |
| Вращение |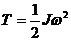 
|
| Поступательное движение |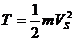 
|
| Плоское движение | 
|
Окончательно
- для механической системы
,
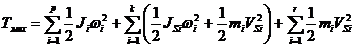где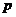 
- число звеньев двигающихся вращательно, 
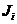- момент инерции этих звеньев относительно точки закрепления, если центр масс не лежит на оси, то применяют теорему Штейнера –Гюйгенса:
,
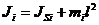где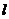 
- расстояние от центра масс звена до оси вращения, 
- момент инерции звеньев относительно центра масс, 
- число звеньев, движущихся плоско, 
- число звеньев движущихся поступательно.
- для модели (вращающейся)
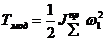
Модель будет энергетически эквивалентна рассматриваемой механической системе, если правые и левые части уравнений изменения кинетической энергии для модели и для системы будут соответственно равны.
Подставляя в равенства, записанные ранее выражения для кинетических энергий, получим:
|
|
|
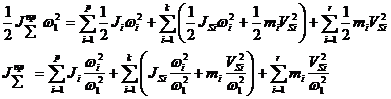
Из уравнения для левых частей получаем формулу для определения приведенного суммарного момента инерции динамической модели
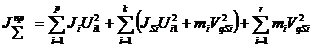
В любом машинном агрегате приведенный суммарный момент инерции динамической модели состоит из 2-х частей:
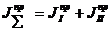
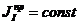- приведенный момент инерции первой группы звеньев. К первой группе звеньев относятся те звенья, которые имеют постоянное передаточное отношение со звеном приведения.
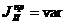- приведенный момент инерции второй группы звеньев. Ко второй группе звеньев относятся те звенья, которые не имеют постоянного передаточного отношения со звеном приведения.
