Запишем для динамической модели теорему об изменении кинетической энергии в дифференциальной форме:
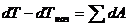 ,
,
Так как: 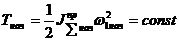 ,
, 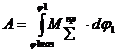 ,
, 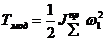 ,
,
то 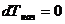 ,
, 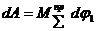 и
и 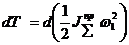 .
.
Подставим в исходное уравнение: 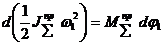
и разделим правую и левую часть на 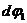 :
:
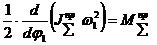 .
.
Учитывая, что 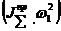 - функции положения, т.е. зависят от
- функции положения, т.е. зависят от 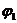 , запишем дифференциал левой части:
, запишем дифференциал левой части:
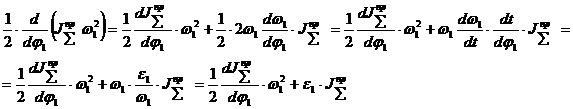
и уравнение движения динамической модели в дифференциальной форме:
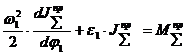
Из этого уравнения после преобразований получим формулу для расчета углового ускорения звена приведения:
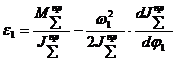
Для механических систем, в которых приведенный момент не зависит от положения звеньев механизма, т.е. 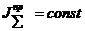
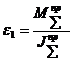 .
.
Аналогично при приведении к поступательно движущемуся звену или точке, может быть получена формула для расчета ускорения:
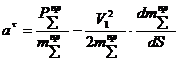 .
.
Для механических систем, в которых приведенная масса не зависит от положения звеньев механизма, т.е. 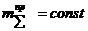
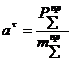 .
.
.
 2017-12-16
2017-12-16 14396
14396








