Математическое ожидание и его свойства

Мат. Ожидание случайной величины (средневзвешенное значение случайной величины) является аналогом такой физической величины как центр тяжести.

Свойства:

1. MC=C

2. M(CX)=C*MX

3. M(X+Y)=MX+MY

4. M(X*Y)=MX*MY, еслиXи Y независимые

Дисперсия и ее свойства

Дисперсией называется математическое ожидание отклонения случайной величины от среднего значения.

Свойства:

1.

2. DX≥0

3.

4. D(X+C)=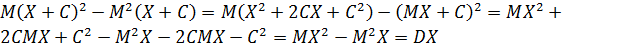

5. Формула Дисперсии суммы:

R_x,y– корреляционный момент x,y

ИТОГ Свойства 5:

Если x,y – независимы, то R_x,y=0 и D(X+Y)=DX+DY

Нормированные случайные величины

Показательное распределение

Биномиальное распределение

MX=npDX=npq

Равномерное распределение (вопрос)

 

 

 

Нормальное распределение. Правило 3-х сигм

Нормальный закон распределения также называется законом Гаусса. Нормальный закон распределения занимает центральное место в теории вероятностей. Это обусловлено тем, что этот закон проявляется во всех случаях, когда случайная величина является результатом действия большого числа различных факторов. К нормальному закону приближаются все остальные законы распределения.

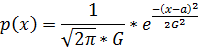
Правило 3-х сигм