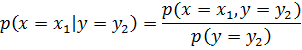
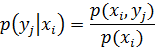
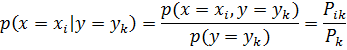
Условной плотность f(x|y) распределения составляющих Xпри заданном значении Y=y называется отношение плотности совместного распределения f(x,y) системы (X,Y) к плотности распределения 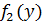 составляющей Y
составляющей Y
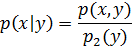
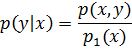
Или
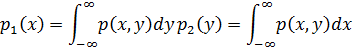
Условным математическим ожиданием дискретной случайной величины Yпри X=x (x–определенное системное значение X) называется произведение возможных значений Yна их условные вероятности
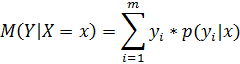
Формула Ассаула: 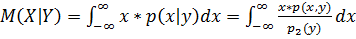
Регрессия
M(Y|X)=f(x) называется функцией регрессии Yна X
Регрессией Yна X называется зависимость условного мат. Ожидания M(Y|X) от значения X
Регрессией Xна Y называется зависимость условных мат. Ожиданий M(X|Y) от значения Y
Графики этих зависимостей называются линиями регрессий Y наX илиX наY.
Неравенства Чебышева(проверить знаки)
Неравенства Чебышева справедливо для дискретных и непрерывных случайных величин
Условие: x>0
Неравенство 1: 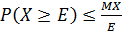
Неравенство 2: 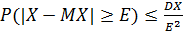
Следствия из 2-ого неравенства:
Первое: 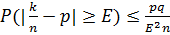
Второе (для проведения измерений): 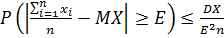
Теорема Чебышёва (док-во понять)
Если 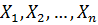 – попарно независимые случайные величины, причем их дисперсии равномерно ограничены (не превосходят постоянного числа – константы), то как бы мало не было положительное число Е, вероятность неравенства равна:
– попарно независимые случайные величины, причем их дисперсии равномерно ограничены (не превосходят постоянного числа – константы), то как бы мало не было положительное число Е, вероятность неравенства равна:
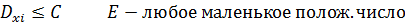
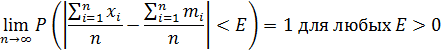
Доказательство:
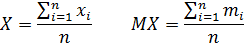
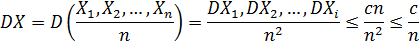
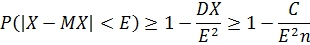
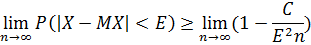
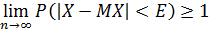
 2017-12-16
2017-12-16 1155
1155
