Формула полной вероятности (вопрос)

Рассмотрим некоторую систему событий H₁,…,H_n. Если эти события попарно несовместны, а их объединение равно достоверному событию, то такие события называются Гипотезами.

Рассмотрим некоторую систему гипотез к некоторому эксперименту, который можно повторить и произв. Событие А.

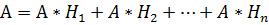(попарно несов.)

=>

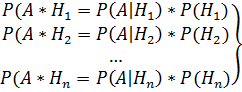
И в итоге получаем Формулу полной вероятности:

Формула Байеса.

Для зависимых событий:

Формула:

Испытания Бернулли. Наиболее вероятное число успехов (вопрос)

Испытания Бернулли – это последовательные повторные независимые испытания.

В каждом испытании p – вероятность успеха, q–вероятность неудачи (q= 1-p)

–вероятность, что все из nиспытаний будут иметь kуспеха.

Наиболее вероятное число успехов

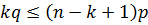
ИТОГ: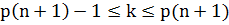

Локальная теорема Муавра-Лапласа

Локальная теорема Муавра — Лапласа. Если в схеме Бернулли число n велико (n>10), а число p отлично от 0 и 1, тогда:

Где: 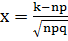и (все значения этой функции даны в таблице)

Функция называется функцией Гаусса.

Функция Гаусса обладает двумя свойствами, которые следует учитывать при работе с таблицей значений:

1. φ(−x) = φ(x) — функция Гаусса — четная;

2. При больших значениях x имеем: φ(x) ≈ 0.

Интегральная теорема Лапласа

Свойства Фo:

1. Нечетная функция (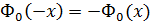

2.

3.