Тройка векторов называется упорядоченной, если каждому из них присваивается порядковый номер.
Упорядоченная тройка ненулевых и некомпланарных векторов называется правой, если после приведения их к общему началу из конца третьего вектора кратчайший поворот от первого ко второму виден совершающимся против часовой стрелки. В противном случае тройка векторов называется левой.
Примером правой тройки векторов является тройка ортов  .
.
Определение. Векторным произведением вектора  на вектор
на вектор  называется вектор
называется вектор  , который определяется тремя условиями:
, который определяется тремя условиями:
1. 

 2.
2. 
 и
и 
 , т.е.
, т.е. 
3. Векторы  ,
,  и
и  , взятые в указанном порядке, образуют правую тройку векторов.
, взятые в указанном порядке, образуют правую тройку векторов.
 Если хотя бы один из векторов
Если хотя бы один из векторов  или
или  нулевой, то полагают
нулевой, то полагают  =
=  по определению.
по определению.
Рассмотрим свойства векторного произведения.
|
20. Векторное произведение равно нулевому вектору тогда и только тогда, когда векторы коллинеарны. В частности,  =
=  .
.
30. Также из определения непосредственно следует, что векторное произведение антикоммутативно, т.е.  =
=  для любых векторов
для любых векторов  и
и  .
.
40. Векторное произведение сочетательно по отношению к скалярному множителю, т.е. 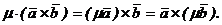
Действительно, направления всех трех векторов одинаковы, как на рис. 11, где μ<0.
И по определению модули всех трех векторов равны между собой: 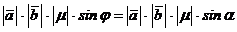 , где α = π – φ и потому sin α = sin φ.
, где α = π – φ и потому sin α = sin φ.
Очевидно, сочетательное свойство остается в силе и тогда, когда векторы  и
и  коллинеарны либо μ = 0.
коллинеарны либо μ = 0.
50. Векторное произведение дистрибутивно относительно сложения векторов: 
Доказательство. Утверждение очевидно справедливо при  Пусть
Пусть 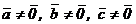 .
.
Выберем прямоугольную декартову систему координат xyz, в которой данные неколлинеарные векторы  отложены от начала О и определяют координатную плоскость yz. Выполним сложение векторов
отложены от начала О и определяют координатную плоскость yz. Выполним сложение векторов  по правилу параллелограмма:
по правилу параллелограмма:  (рис. 12).
(рис. 12).
 По определению найдем векторные произведения:
По определению найдем векторные произведения:
 (*)
(*)
|
 получен поворотом вокруг начала координат в плоскости yz соответствующего ему вектора
получен поворотом вокруг начала координат в плоскости yz соответствующего ему вектора  на один и тот же угол π/2. При таком повороте параллелограмм, построенный на векторах
на один и тот же угол π/2. При таком повороте параллелограмм, построенный на векторах  с диагональю
с диагональю  , переходит в равный ему параллелограмм, построенный на векторах
, переходит в равный ему параллелограмм, построенный на векторах  с диагональю
с диагональю  . Воспользуемся этим равенством и результатами (*).
. Воспользуемся этим равенством и результатами (*). 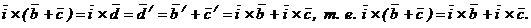
Обе части последнего равенства умножим на число  . В силу сочетательности векторного произведения по отношению к скалярному множителю получим:
. В силу сочетательности векторного произведения по отношению к скалярному множителю получим:
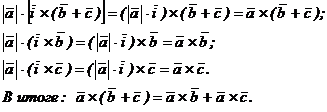
Последнее алгебраическое свойство 50 векторного произведения дает право при перемножении векторных многочленов выполнять действия почленно, а свойство 40 позволяет объединять числовые коэффициенты векторных сомножителей. Например,

Следует, однако, еще раз напомнить, что порядок сомножителей векторного произведения является существенным и при перестановке сомножителей знак векторного произведения нужно изменить.
Задача 0.42. Доказать, что если  , то
, то 
Доказательство.
Умножим векторно  на
на  .
.
Получим 

Умножим векторно  на
на  . Получим
. Получим 

Из двух полученных равенств следует, что 
Задача 0.43. Вычислить площадь параллелограмма, построенного на векторах 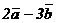 и
и  , если
, если 
Решение. По определению векторного произведения  =(
=(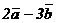 )×(
)×( ) площадь S параллелограмма, построенного на векторах
) площадь S параллелограмма, построенного на векторах 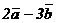 и
и  равна
равна  , т.е. S =
, т.е. S =  . Найдем
. Найдем  , учитывая, что векторное произведение сочетательно по отношению к скалярному множителю и дистрибутивно относительно сложения векторов.
, учитывая, что векторное произведение сочетательно по отношению к скалярному множителю и дистрибутивно относительно сложения векторов.
 =(
=( )×(
)×(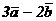 )= 6
)= 6  .
.
Таким образом,  =
=  =
= 
Ответ:  кв.ед.
кв.ед.
 2017-12-16
2017-12-16 1440
1440
