2017-12-16
1360
Пусть заданы векторы 
. Вектор 
умножим скалярно на вектор 
.
Получим: 
или
Задача 0.47. Найти объем тетраэдра с вершинами А(2; 2; 2), В(4; 4; 3), С(4; 5; 4) и D(5; 5; 6) и высоту, опущенную из вершины А на грань ВСD.
Решение. Вычислим координаты векторов, приложенных к точке D..
 |
Найдем векторное произведение 
, половина модуля которого равна площади треугольника ВСD.
Следовательно, SBCD=0,5 
.
Объем тетраэдра АВСD равен 
части объема параллелепипеда, построенного на векторах 
и равен части модуля смешанного произведения этих векторов.
.
Следовательно, объем V тетраэдра равен 
.
Высоту AQ тетраэдра найдем из соотношения 
. Получим 
.
Ответ: V= 
куб.ед; 
.
Задача 0.48. Решите систему уравнений:
Решение. В прямоугольной системе координат xyz рассмотрим векторы 
Тогда систему уравнений можно рассматривать как координатную запись векторного равенства 
, где векторы 
не компланарны, т.к.
.
Обе части векторного равенства умножим скалярно на вектор 
. Получим 
и тогда первое уравнение системы заменим уравнением 
= 
Аналогично заменим остальные уравнения исходной системы и получим эквивалентную ей систему уравнений:
Вычислим смешанные произведения. 
.
Система уравнений принимает вид: 
Ответ: (2; 1; -2).
§ 10. Упражнения
№ 1. Изобразите какие-нибудь векторы 
. Постройте векторы: 1). 
;
2). 
; 3). 
; 4). 
.
№ 2. Векторы 
, 
и 
выразите через векторы 
и 
.
Ответ: 
№ 3. Точки A,B,C и D – вершины параллелограмма, О – его центр. Упростите следующие выражения: 1). 
. 2). 
. 3). 
.
Ответ: 1) 
2) 
3) 
№ 4. Какому условию должны удовлетворять векторы 
и 
, чтобы: 1). выполнялось равенство 
; 2) векторы 
+ 
и – были коллинеарны?
Ответ: 1) 
2) 
║ 
.
№ 5. При каком k справедливо соотношение 
Ответ: k = -1.
№ 6. Векторы 
и 
служат двумя смежными сторонами правильного шестиугольника ABCDEF с центром O. Выразите через 
и 
векторы 
и 
.
Ответ: 
№ 7. Пусть К и М – середины сторон ВС и СD соответственно параллелограмма АВСD и 
. Выразите векторы 
через векторы 
.
Ответ: 
№ 8. Диагонали выпуклого четырехугольника ABCD пересекаются в точке O. Известно, что существует четырехугольник, стороны которого равны и параллельны отрезкам OA, OB, OC и OD соответственно. Докажите, что ABCD – параллелограмм.
№ 9. В треугольнике ABC проведены медианы AD, BE, и CF. Найдите сумму 
.
Ответ: 
.
№ 10. Доказать, что четырехугольник ABCD – параллелограмм, если верно равенство 
для любой точки O и точки A, B, C и D не лежат на одной прямой.
№ 11. Из точки O выходят два вектора 
и 
. Найдите какой-нибудь вектор 
, идущий по биссектрисе угла AOB.
Ответ: 
№ 12. Доказать, что точки А(1;8), В(-2;-7) и С(-4;-17) лежат на одной прямой. Какая из них лежит между двумя другими?
Ответ: Точка В лежит между точками А и С.
№ 13. Три точки M(7;8), N(-4;5) и E(1;4)- середины сторон АВ, ВС, АС соответственно в треугольнике АВС. Найти координаты точек А, В и С и длину медианы AN.
Ответ: А (12; 7), B (2; 9), С (-10; 1); 
№ 14. К вершине куба приложены три силы, равные по величине 1, 2 и 3 и направленные по диагоналям граней куба. Определить величину равнодействующей.
Ответ: 
№ 15. Точка D делит отрезок АС в отношении –2. Найти координаты точки D, если А(-8; 0; 2) и С(3; -2; 0).
Ответ: 
№ 16. Найти на отрезке, соединяющем точки О(0; 0; 0) и А(1; 2; 2), точку М, делящую этот отрезок в отношении 2:3.
Ответ: 
№ 17. Даны точки М, А, В и точка С взята так, что 
. Выразите вектор 
через векторы 
.
Ответ: 
№ 18. Отрезок, определяемый точками А(-6;7) и В(-2;3), разделен на 4 равные части. Найти точки деления L, M и N. До какой точки Р нужно продолжить отрезок АВ, чтобы его длина увеличилась в 3 раза?
Ответ: L (-5; 6), M (-4; 5), N (-3; 4); P (6, -5).
№ 19. Отрезок с концами А(1; -5) и В(4; 3) разделен на 3 равные части. Определить координаты точек деления.
Ответ: 
№ 20. AD – биссектриса внутреннего угла А в треугольнике АВС. Найти координаты точки D, если А(n;1), B(-1;1) и С(n; -n).
Ответ: 
№ 21. В треугольнике ABC проведена биссектриса AD угла A. Выразите вектор 
через векторы 
и 
.
Ответ: 
№ 22. AD – биссектриса внутреннего угла А треугольника АВС. Найти координаты точки D, если 
.
Ответ: D (4n; n).
№ 23. Даны вершины треугольника: А(-2; 0), В(3;-2) и С(1; 4).Найти координаты вершин гомотетичного ему треугольника А1В1С1, если коэффициент гомотетии к= - 2 и центром гомотетии является точка Q = (-4; 4).
Ответ: 
№ 24. Дан треугольник с вершинами А(-7; 7), В(3; 2) и С(-1; -1). Найти точки, в которых сторона АВ пересекается биссектрисами внутреннего и внешнего углов при вершине С.
Ответ: 
. Указание: 
.
№ 25. В треугольнике с вершинами А(-2; 1), В(2;-1) и С(4; 3) найти точку пересечения медиан.
Ответ: 
№ 26. Найти центр тяжести треугольника с вершинами А(3n – 8;-2;3),
B(4;3n – 8;-2) и С(7;-2;8 – 3n).
Ответ: М (n + 1; n – 4; 3 – n).
№ 27. Найти центр тяжести треугольника с вершинами А(n; -2), В(4;n) и С(7; -2).
Ответ: M (4; -1).
№ 28. В точках A(x1) и B(x2) сосредоточены массы m1 и m2 соответственно. Найти координаты центра тяжести этой системы материальных точек.
Ответ: 
№ 29. Найти координаты центра тяжести масс 3 и 5, сосредоточенных в точках A(3; -5) и B(-1; 1).
Ответ: 
№ 30. Даны векторы 
. Найти вектор 
, где М – центр тяжести треугольника АВС.
Ответ: 
№ 31. Найти координаты, модуль и направляющие косинусы вектора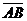 
, если известны координаты точек: 1). A(2; n;4) и B(3; 7; 5). 2). А(n; 2; 5) и В(4; 4; 0).
Ответ: 1) 
; 
; 
; 
; 
; 2) 
; 
; 
; 
; 
.
№ 32. Пользуясь понятием проекции вектора на вектор, найти длины отрезков, на которые высота, опущенная из вершины В(2; 0; -2) треугольника АВС, делит сторону АС с концами А(3; 5; 6) и С(3; 4; -6).
Ответ: 
; 
№ 33. Найти проекцию вектора 
на ось e, которая составляет с координатными осями x, y и z углы α0, β0, γ0 соответственно.
Ответ: 
№ 34. Найти проекцию вектора 
= (2; 5; 1) на ось e, составляющую с координатными осями равные острые углы.
Ответ: 
№ 35. Найти проекцию вектора 
на направление вектора 
, если 
, 
, 
и 
.
Ответ: 
№ 36. Найти проекцию вектора 
на направление вектора 
, если 
, 
Ответ: 
№ 37. Известно, что 
, 
, 
. Найти 
.
Ответ: 
№ 38. Найти скалярное произведение векторов = (2; 1; -3) и = (5; -4; 2), угол между ними и проекцию вектора 
на направление вектора 
.
Ответ: 
; 
№ 39. Даны векторы 
и 
. Найдите длины диагоналей параллелограмма, построенного на векторах 
и если 
и 
.
Ответ: 
№ 40. Даны векторы и такие, что 
, 
, 
. Найти 
.
Ответ: 
= 20.
№ 41. Найти вектор , являющийся ортогональной проекцией вектора
= (1, 4, 8) на прямую, параллельную вектору = (1, 2,-2).
Ответ: 
.
№ 42. Даны векторы 
. Найти вектор 
Ответ: 
.
№ 43. Даны векторы 
=(-n,-2), =(-2,n), =(0,4). Найдите вектор 
.
Ответ: 
№ 44. Пусть векторы 
перпендикулярны. При каком значении параметра μ вектор 
перпендикулярен вектору 
?
Ответ: 
.
№ 45. Доказать, что треугольник АВС тупоугольный, если его вершинами являются точки А(2; 3), В(6; 7) и С(-7; 2).
№ 46. Найти угол между диагоналями параллелограмма, построенного на векторах 
.
Ответ: 
№ 47. Найти косинус внутреннего угла А в треугольнике с вершинами А(2; 3; 1),
В(1; 4; 0) и С(-1; 1; 1).
Ответ: 
№ 48. Найти вектор если = (1; -n; -2), 
; 
= (2; n; 3), 
, 
и 
Ответ: 
№ 49. Найти вектор 
, зная, что он перпендикулярен векторам 
и удовлетворяет условию 
где 
Ответ: 
.
№ 50. Найти вектор 
, перпендикулярный векторам 
если известно, что он образует с осью у острый угол и его длина равна 
.
Ответ: 
№ 51. Дан равносторонний треугольник ABC, длина стороны которого равна 1. Полагая 
, 
и 
, вычислите 
.
Ответ: 
№ 52. Известно, что векторы 
и 
взаимно перпендикулярны. Какой угол образуют единичные векторы 
и 
?
Ответ: 
№ 53. Может ли вектор составлять с осями координат углы 
и 
в системе xyz?
Ответ: Не может.
№ 54. Вычислите 
, если 
и 
.
Ответ: 
№ 55. Вычислить косинус тупого угла, образованного медианами, проведенными из вершин острых углов равнобедренного прямоугольного треугольника. Ввести систему ху.
Ответ: 
.
№ 56. Найти угол при вершине С равнобедренного треугольника ABC (AC = BC), если медианы, проведенные к его боковым сторонам, взаимно перпендикулярны.
Ответ: Ð С = arccos 0,8. Указание: Расположить треугольник на координатной плоскости ху.
№ 57. В призме ABCA1B1C1 найти угол между диагональю AC1 боковой грани и медианой AM основания, если A(-1; 3; 4),B(4; 4; 2), C(0; 2; 0), C1(1; 4; 3).
Ответ: 
№ 58. Концы А(9; 6; 4), В(3; 0; 4) и С(5; 2; 6) ребер параллелепипеда соединены с вершиной М(1; 2; 3). Найти косинус угла между диагональю МD параллелепипеда и его ребром МА.
Ответ: 
№ 59. Найти противоположно направленный вектору 
вектор , если 
.
Ответ: 
№ 60. Какую работу производит равнодействующая сил 
, приложенных к точке М(4; 2; -8), когда эта точка перемещается в точку N(n; -2; -5)?
Ответ: 19 ед. работы.
№ 61. Найти единичный вектор, перпендикулярный векторам 
и 
Ответ: 
№ 62. Найти вектор 
, зная, что он перпендикулярен векторам 
и 
и удовлетворяет условию 
где 
.
Ответ: 
№ 63. Вычислить площадь параллелограмма, построенного на векторах 
и 
, если 
Ответ: S = 2· 
кв. ед. Указание: найти модуль векторного произведения.
№ 64. Векторы 
определены координатами своих концов А(-3; 1; 0),
В(-1; -1; -2),С(-2; 2; 0) и D(-5; 1; 1). Найти вектор 
, его направляющие косинусы и площадь треугольника АВС.
Ответ: 
; 
, 
, 
.
№ 65. Найти угол между диагоналями параллелограмма, построенного на векторах 
и 
, отнесенных к одной точке. Найти площадь этого параллелограмма.
Ответ: 
№ 66. На векторах 
= (2; 3; 1) и 
=(-1; 1; 2), отложенных от одной точки, построен треугольник. Найти длины трех его высот.
Ответ: 
№ 67. Дан треугольник с вершинами А(-n; 0), В(0; -2) и С(n; 2). Точка D делит отрезок АС в отношении -3. Найти координаты точки D и вычислить площадь треугольника АВD.
Ответ: 
; SАВД = 30.
№ 68. Даны две точки: L(3; 5) и M(6; -2). На оси y найти такую точку N, чтобы площадь треугольника LMN равнялась 15 кв. ед.
Ответ: 
или 
.
№ 69. Даны вершины А(2; 1), В(-2; -2) и С(-8; 6) треугольника. Найти длину высоты, опущенной из вершины В.
Ответ: 
№ 70. Три силы 
приложены к точке В(3; -n; 8). Определить модуль и направляющие косинусы момента равнодействующей этих сил относительно точки А(4; -2; 6).
Ответ: 
; 
, 
. Указание: 
.
№ 71. Показать, что точки А(5; n; -2), В(3; -n; -1), С(9; n; -4) и D(1; -n; 0) лежат в одной плоскости.
№ 72. Найти единичный вектор 
, перпендикулярный векторам 
и направленный так, чтобы тройка векторов 
была правой.
Ответ: 
№ 73. Показать, что векторы 
и 
компланарны.
№ 74. Вычислить длину высоты, опущенной из вершины А1 параллелепипеда АВСДА1В1С1Д1 на его основание АВСД, если А(n; -1; -n), В(2n; 1; n), С(0; -2; -n) и А1(-n; 0; 3).
Ответ: 
.
№ 75. Лежат ли точки А(-1;n;0), B(1;2n;0), C(1;0;0) и Q(-n;n;1) в одной плоскости? Если нет, то каков объем тетраэдра QABC и его высота, опущенная из вершины Q?
Ответ: Не лежат. 
Н=1.
№ 76. Объем треугольной пирамиды равен 9 куб. ед. Три ее вершины находятся в точках А(4; -1; 2), В(5; 1; 4) и С(3; 2; -1). Найти координаты четвертой вершины D, если она находится на оси z.
Ответ: 
или 
.
