Тема 3. Векторная алгебра.
Основные понятия.
Понятие вектора исторически сложилось как математическая абстракция объектов, характеризующихся и величиной и направлением, таких, как сила, скорость, ускорение, перемещение, напряженность магнитного или электрического поля и др.
Вектором называетсяупорядоченная пара точек или, что то же самое, направленный отрезок.
 А В
А В
Один конец отрезка (точку А) назовем началом вектора, а другой его конец (точку В) – концом вектора. Обозначается такой вектор символом 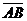 и характеризуется длиной, которая равна расстоянию между точками A и B, и направлением от A к B, которое указывают стрелкой в конце B отрезка AB. Длина вектора обозначается символом
и характеризуется длиной, которая равна расстоянию между точками A и B, и направлением от A к B, которое указывают стрелкой в конце B отрезка AB. Длина вектора обозначается символом  и еще называется модулем вектора или его абсолютной величиной.
и еще называется модулем вектора или его абсолютной величиной.
Вектор 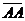 , у которого начало и конец совпадают, называется нулевым и обозначается символом
, у которого начало и конец совпадают, называется нулевым и обозначается символом 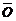 . Модуль нулевого вектора равен нулю, а направление произвольно.
. Модуль нулевого вектора равен нулю, а направление произвольно.
Ненулевые векторы называют коллинеарными, если они лежат на одной прямой или на параллельных прямых. Нулевой вектор коллинеарен любому вектору.
Два коллинеарных вектора называют одинаковонаправленными либо противоположно направленными, если они помещены в одной плоскости и их концы лежат соответственно по одну либо разные стороны от прямой, содержащей их начала.
Два противоположно направленных вектора одинаковой длины называют противоположными. Примером могут служить векторы 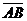 и
и  .
.
Ненулевые векторы называют компланарными, если прямые, их содержащие, параллельны одной и той же плоскости или принадлежат ей. Любые два вектора компланарны. Если среди трех векторов какие - либо два коллинеарны, либо хотя бы один нулевой, то такие три вектора компланарны.
Два коллинеарных вектора называются равными, если они одинаково направлены и имеют равные модули. Иначе говоря, равными считаются векторы, совмещаемые параллельным переносом. Следовательно, выбрав любую точку М, мы можем построить, и притом только один, вектор  , равный некоторому заданному вектору
, равный некоторому заданному вектору 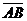 , или, как говорят, перенести вектор
, или, как говорят, перенести вектор 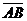 в точку М.
в точку М.
Все нулевые векторы считаются равными.
Условимся не различать равные векторы и таким образом приходим к понятию свободного вектора. Для свободных векторов каждый вектор можно заменить равным ему вектором с началом в любой точке.
Углом между ненулевыми векторами называется угол между сонаправленными с ними векторами с общим началом. Угол между векторами  обозначается символом
обозначается символом  .
.
§ 2. Линейные операции над векторами.
 10. Сложение двух ненулевых векторов определяется правилом трех точек: если конец вектора
10. Сложение двух ненулевых векторов определяется правилом трех точек: если конец вектора 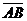 совмещен с началом вектора
совмещен с началом вектора  , то вектор
, то вектор  называется суммой векторов
называется суммой векторов 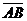 и
и  .
.
|
Из правила трех точек следует правило поглощения нулевого вектора: 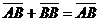 , т.е.
, т.е.  .
.
20. Для каждого вектора 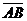 существует противоположный ему вектор
существует противоположный ему вектор  и по правилу трех точек сумма противоположных векторовравна нулевому вектору:
и по правилу трех точек сумма противоположных векторовравна нулевому вектору: 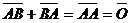 .
.
30. Если векторы 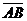 и
и  коллинеарны, то, расположив их на одной прямой, замечаем, что вектор
коллинеарны, то, расположив их на одной прямой, замечаем, что вектор  , если он не нулевой, находится на этой же прямой
, если он не нулевой, находится на этой же прямой

и одинаково направлен с большим по модулю вектором. Модуль вектора  равен сумме модулей векторов
равен сумме модулей векторов 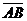 и
и  , если они одинаково направлены, и разности модулей векторов
, если они одинаково направлены, и разности модулей векторов 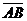 и
и  , если они противоположно направлены.
, если они противоположно направлены.

40. Следствием правила трех точек является правило параллелограмма: если векторы 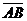 и
и  – стороны параллелограмма ABCD, то их суммой является вектор
– стороны параллелограмма ABCD, то их суммой является вектор  – диагональ этого параллелограмма.
– диагональ этого параллелограмма.
 |
|

Рис. 3
Из правила параллелограмма следует коммутативность сложения векторов:  .
.

 и
и  отложены от одной точки A и являются ребрами параллелепипеда АBCDA1B1C1D1, то их суммой является вектор
отложены от одной точки A и являются ребрами параллелепипеда АBCDA1B1C1D1, то их суммой является вектор  – диагональ этого параллелепипеда.
– диагональ этого параллелепипеда.  |
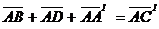
Рис. 4
Из правила параллелепипеда следует ассоциативность сложения векторов: 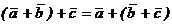 .
.

 60. В общем случаесуммой нескольких векторов называют вектор, замыкающий ломаную, построенную на этих векторах:
60. В общем случаесуммой нескольких векторов называют вектор, замыкающий ломаную, построенную на этих векторах:
Рис. 5
Такая сумма векторов равна нулевому вектору тогда и только тогда, когда ломаная замкнута, т.е. конец последнего вектора совпадает с началом первого.
 70. Вычитание векторов определяется как действие, обратное сложению. Разностью векторов
70. Вычитание векторов определяется как действие, обратное сложению. Разностью векторов  и
и  называют вектор
называют вектор  , который в сумме с вектором
, который в сумме с вектором  дает вектор
дает вектор  , т.е.
, т.е.  , если
, если  .
.
Рис. 6
Следует иметь ввиду, что если векторы сложены по правилу параллелограмма и суммой их является одна диагональ, то вторая диагональявляется их разностью.
80. Задача 0.32. Найти величину равнодействующей двух сил  и
и  , модули которых равны 5 и 7 и угол между ними φ равен 600. Определить также углы α и β, образуемые равнодействующей с силами
, модули которых равны 5 и 7 и угол между ними φ равен 600. Определить также углы α и β, образуемые равнодействующей с силами  и
и  соответственно.
соответственно.
Решение. Построим параллелограмм ABCD и введем обозначения на рисунке.
По теореме косинусов найдем величину равнодействующей  .
.

 Углы α и β вычислим, воспользовавшись теоремой синусов.
Углы α и β вычислим, воспользовавшись теоремой синусов.


Контроль: 
Ответ:  ≈ 10,44; α ≈
≈ 10,44; α ≈  ; β ≈
; β ≈  .
.
90. Произведением ненулевого вектора  и действительного числа μ ¹ 0 называют вектор μ
и действительного числа μ ¹ 0 называют вектор μ  , длина которого равна
, длина которого равна 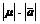 , а направление совпадает с направлением вектора
, а направление совпадает с направлением вектора  , если μ > 0, и противоположно ему, если μ < 0.
, если μ > 0, и противоположно ему, если μ < 0.
Умножение вектора на число обладает следующими свойствами.
Для любых векторов  и
и  и любых действительных чисел μ и λ:
и любых действительных чисел μ и λ:
1). μ  =
=  μ
μ
2). 
3). μ ·  = 0 ·
= 0 ·  =
= 
4). 1 ·  =
= 
5). Вектор -1 ·  = -
= -  противоположен вектору
противоположен вектору  и
и  + (-
+ (-  ) =
) =  -
-  =
=  .
.
6). 
Докажем свойства 6). Числа μ и λ полагаем отличными от нуля и векторы  и
и  отличными от нулевых. В противном случае теорема очевидно верна.
отличными от нулевых. В противном случае теорема очевидно верна.
а). Если  , то все три числа
, то все три числа  ,
,  и
и  +
+  имеют одинаковые знаки, поэтому векторы
имеют одинаковые знаки, поэтому векторы 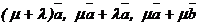 сонаправлены. Для модулей же сонаправленных векторов верны равенства:
сонаправлены. Для модулей же сонаправленных векторов верны равенства:
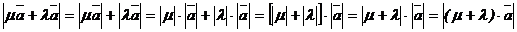 ,т.е.
,т.е.  =
=  .
.
Следовательно,  , т.к. векторы
, т.к. векторы  и
и  сонаправлены и имеют равные модули.
сонаправлены и имеют равные модули.
б). Если μ·λ<0 и, например, λ<0 и λ+μ<0, т.е.  , то -μ<0 и по доказанному
, то -μ<0 и по доказанному
-μ  +(μ+λ)·
+(μ+λ)·  = (-μ+μ+λ)·
= (-μ+μ+λ)·  = λ
= λ  , откуда следует
, откуда следует  =
=  .
.
в). Сложим векторы  =
=  и
и  по правилу трех точек:
по правилу трех точек:

|
 Построим ΔОА1В1, гомотетичный треугольнику ОАВ с центром гомотетии О и коэффициентом гомотетии
Построим ΔОА1В1, гомотетичный треугольнику ОАВ с центром гомотетии О и коэффициентом гомотетии μ ¹ 0. Получим:
 ,
,  и
и  . Но по правилу трех точек
. Но по правилу трех точек  , т.е.
, т.е.  или
или  .
. Таким образом, умножение вектора на число дистрибутивно как относительно сложения чисел, так и относительно сложения векторов.
100. Вектор  , сонаправленный с вектором
, сонаправленный с вектором  , называется ортом вектора
, называется ортом вектора  , если
, если  .
.
По определению умножения вектора на число любой вектор  можно представить в виде произведения его модуля и орта:
можно представить в виде произведения его модуля и орта:  =
=  . Замена вектора
. Замена вектора  его ортом
его ортом  называется нормированием вектора
называется нормированием вектора  .
.
По определению векторы  и
и 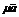 коллинеарны. Верно и обратное утверждение. Если два вектора
коллинеарны. Верно и обратное утверждение. Если два вектора  и
и  коллинеарны, то один из них можно получить из другого умножением на число.
коллинеарны, то один из них можно получить из другого умножением на число.
Действительно, для коллинеарных векторов их орты  и
и  имеют равные модули и либо сонаправлены, либо противоположно направлены. Поэтому
имеют равные модули и либо сонаправлены, либо противоположно направлены. Поэтому 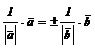 и тогда
и тогда  .
.
Задача 0.33. В треугольнике АВС проведены медианы AD, BE, CF. Для произвольной точки Q выразите векторы  ,
,  и
и 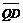 через векторы
через векторы  ,
,  и
и  .
.
 Решение. Воспользуемся определениями и свойствами линейных операций над векторами (см. рисунок).
Решение. Воспользуемся определениями и свойствами линейных операций над векторами (см. рисунок).
1.  .
.
2.  .
.
3.  .
.
Ответ:  ;
;  ;
; 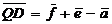 .
.
§ 3. Проекция вектора на ось. Декартовы координаты вектора.
Полагаем, что координатная ось x содержит единичный вектор  с началом в начале координат и направление его совпадает с положительным направлением оси x. Назовем вектор
с началом в начале координат и направление его совпадает с положительным направлением оси x. Назовем вектор  ортом оси x. Очевидно, что координатная ось x однозначно определена своим ортом
ортом оси x. Очевидно, что координатная ось x однозначно определена своим ортом  . Аналогично координатные оси y и z могут быть заданы своими ортами
. Аналогично координатные оси y и z могут быть заданы своими ортами  , а тогда прямоугольная декартова система координат Oxyz однозначно определяется системой попарно перпендикулярных ортов
, а тогда прямоугольная декартова система координат Oxyz однозначно определяется системой попарно перпендикулярных ортов  ,
,  с общим началом.
с общим началом.
Через произвольную точку М проведем плоскость w перпендикулярно координатной оси x. Тогда точка М1 пересечения плоскости с осью является проекцией точки М на ось x. Если координата точки М1 равна числу m, то по определению полагают, что координата любой точки плоскости w относительно оси х также равна m.

|
 не изменятся, если вектор
не изменятся, если вектор  отложить от проекции его начала на ось x.
отложить от проекции его начала на ось x.  Отложим произвольный вектор
Отложим произвольный вектор  от проекции А(α) его начала, а проекцией его конца полагаем точку В(β). Нас будет интересовать разность β-α между координатой конца и координатой начала вектора
от проекции А(α) его начала, а проекцией его конца полагаем точку В(β). Нас будет интересовать разность β-α между координатой конца и координатой начала вектора  при различных значениях угла φ=(
при различных значениях угла φ=( ) между векторами
) между векторами 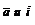 .
.
Если φ=0, то 
Если 0<φ<  , то
, то 
|
 Если φ =
Если φ =  ,то
,то 
Если  <φ<
<φ<  , то
, то 
Если φ=  , то
, то 
=  .
.
Таким образом, для любого значения угла φ из промежутка [0; π] верно равенство

Число  , равное разности между координатами конца и начала вектора
, равное разности между координатами конца и начала вектора  , называют числовой проекцией вектора
, называют числовой проекцией вектора  на направление вектора
на направление вектора  или координатой вектора
или координатой вектора  и пишут
и пишут  .
.
Чтобы показать, что координатой вектора  относительно координатной оси x является некоторое число μ, пишут
относительно координатной оси x является некоторое число μ, пишут  =(μ).
=(μ).
Относительно одной и той же координатной оси равные векторы имеют равные координаты, т.к. все они могут быть совмещены с одним и тем же вектором с началом на оси.
Теорема о проекции вектора на ось.
Для любых векторов  и
и  и любого действительного числа μ верны равенства:
и любого действительного числа μ верны равенства:
1). 
2). 
3). 
Доказательство. Полагаем векторы  и
и  не нулевыми и не перпендикулярными направлению
не нулевыми и не перпендикулярными направлению  . В противном случае теорема очевидно верна.
. В противном случае теорема очевидно верна.
Воспользуемся обозначениями на рисунке 10.

Рис. 10
1. 
 =
= 
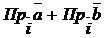
2. Т.к.  , то
, то  =
= 
 +
+  , откуда следует
, откуда следует 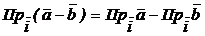
3.  .
.
Если m > 0, то векторы  и
и 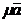 сонаправлены и проекции этих векторов имеют одинаковые знаки. Если m < 0, то проекции векторов
сонаправлены и проекции этих векторов имеют одинаковые знаки. Если m < 0, то проекции векторов  и
и  имеют противоположные знаки. Следовательно, в обоих случаях
имеют противоположные знаки. Следовательно, в обоих случаях  .
.
Теорема доказана.
Если в прямоугольной декартовой системе координат 0xyz задан вектор  и известны числа
и известны числа  , то эти числа а1, а2, а3 называют координатами вектора
, то эти числа а1, а2, а3 называют координатами вектора  : абсцисса а1, ордината а2, аппликата а3. Пишут
: абсцисса а1, ордината а2, аппликата а3. Пишут  =(а1, а2, а3).
=(а1, а2, а3).
Если концами вектора  =
=  являются точки А(x1,y1,z1) и В(x2, y2, z2), то по определению проекциями вектора на координатные оси являются числа x2 - x1, y2 - y1 и
являются точки А(x1,y1,z1) и В(x2, y2, z2), то по определению проекциями вектора на координатные оси являются числа x2 - x1, y2 - y1 и
z2 - z1, поэтому  =(x2-x1, y2-y1, z2-z1).
=(x2-x1, y2-y1, z2-z1).
Заметим, что если начало вектора  совпадает с началом координат О, то координатами вектора
совпадает с началом координат О, то координатами вектора  являются координаты его конца М и вектор
являются координаты его конца М и вектор  называют радиус-вектором точки М. В частности, радиус-векторами являются и орты
называют радиус-вектором точки М. В частности, радиус-векторами являются и орты 
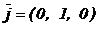 и
и 
Если заданы векторы  =(а1, а2, а3) и
=(а1, а2, а3) и  = (b1, b2, b3), то по теореме о проекции вектора на ось сумма векторов и произведение вектора на число имеют координаты:
= (b1, b2, b3), то по теореме о проекции вектора на ось сумма векторов и произведение вектора на число имеют координаты:
 = (а1+b1, а2+b2, а3+b3),
= (а1+b1, а2+b2, а3+b3),  = (μа1, μа2, μа3).
= (μа1, μа2, μа3).
Следовательно,  =(а1, а2, а3)= (а1,0, 0) + (0, а2,0) + (0, 0, а3) = а1(1, 0, 0) +
=(а1, а2, а3)= (а1,0, 0) + (0, а2,0) + (0, 0, а3) = а1(1, 0, 0) +
+а2(0, 1, 0) + а3(0, 0, 1) = а1  + а2
+ а2  + а3
+ а3  , т.е. произвольный вектор
, т.е. произвольный вектор 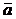 =(а1, а2, а3) можно представить в виде линейной комбинации ортов с коэффициентами а1, а2, а3:
=(а1, а2, а3) можно представить в виде линейной комбинации ортов с коэффициентами а1, а2, а3:
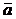 = а1
= а1 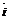 + а2
+ а2  + а3
+ а3  .
.
В таких случаях говорят, что вектор  разложен по ортам
разложен по ортам  .
.
Задача 0.34. Записать разложение вектора 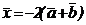 по ортам
по ортам  , если известно, что
, если известно, что


Решение. Найдем координаты вектора  . По определению
. По определению
 =
= 

 /
/
Аналогично  Найдем координаты вектора
Найдем координаты вектора 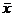 . Т.к. -2
. Т.к. -2  = -2˙(2+3;-2 +0; 1+4) =(-10; 4; -10), то
= -2˙(2+3;-2 +0; 1+4) =(-10; 4; -10), то  и, следовательно,
и, следовательно, 
Ответ: 
Деление отрезка в данном отношении.
Пусть три точки A, B и C принадлежат одной прямой.
Говорят, что точка B делит отрезок AC в отношенииμ, если  . Это равенство предполагает, что если точка В находится между точками А и С (делит отрезок АС внутренним образом), то μ>0; если точка В находится вне отрезка АC (делит его внешним образом), то μ<0; если В º А, то μ=0 и если В º С, то μ не существует.
. Это равенство предполагает, что если точка В находится между точками А и С (делит отрезок АС внутренним образом), то μ>0; если точка В находится вне отрезка АC (делит его внешним образом), то μ<0; если В º А, то μ=0 и если В º С, то μ не существует.
Найдем положение точки В, если положение точек А и С известно.
Для любой точки О верны равенства 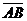 =
=  -
-  и
и 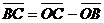 по определению разности векторов. А тогда равенство
по определению разности векторов. А тогда равенство  принимает вид
принимает вид
 -
-  =μ·(
=μ·(  ), откуда получаем
), откуда получаем  + μ ·
+ μ ·  =
=  + μ·
+ μ·  и
и 
Если точку О полагать началом координат, то полученная формула позволяет найти координаты одной из точек А, В и С, если известны координаты двух других точек и число μ, либо найти число μ, если известны координаты всех трех точек.
Так, координаты точки В(х, y, z) по координатам точек А(х1, y1, z1) и С(х2, y2, z2) найдем как координаты вектора:

В частности, если В– середина отрезка АС, то 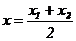 ,
,  ,
, 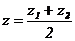 .
.
Задача 0.35. Точка P делит отрезок AB с концами A(x1) и B(x2) в отношении μ. Точка Q делит тот же отрезок в отношении - μ. В каком отношении середина R отрезка PQ делит отрезок AB?
Решение. Известно из условия задачи, что  ,
,  и
и  , а тогда
, а тогда



Ответ: – μ2.
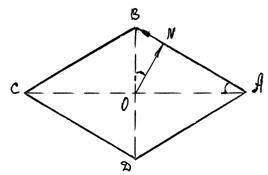
Задача 0.36. Угол А ромба ABCD равен 600. Из центра O этого ромба опущен на его сторону AB перпендикуляр OM. Выразите вектор  через векторы
через векторы  и
и  .
.
|
|
 , откуда
, откуда  и тогда
и тогда  или
или  .
.
Найдем векторы  и
и  :
:
1).  и тогда
и тогда
 .
.
2).  .
.
В итоге 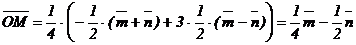 .
.
Ответ:  .
.
Задача 0.37. В каком отношении точка В(4;-1) делит отрезок с концами А(-4; 3) и С(1; 0,5)?
Решение. Полагаем, что точка В делит отрезок АС в отношении  , т.е.
, т.е.  . Тогда координаты этих точек связаны соотношениями
. Тогда координаты этих точек связаны соотношениями  каждое из которых дает нам
каждое из которых дает нам  . Ответ: -8:3
. Ответ: -8:3
 2017-12-16
2017-12-16 2861
2861