Направляющие косинусы и длина вектора.
Скалярным произведением ненулевых векторов  и
и 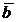 называют число (скаляр), равное произведению модулей этих векторов на косинус угла φ между ними:
называют число (скаляр), равное произведению модулей этих векторов на косинус угла φ между ними:
 .
.
Если хотя бы один из векторов  или
или  нулевой, то угол φ не определен и скалярное произведение по определению полагают равным нулю.
нулевой, то угол φ не определен и скалярное произведение по определению полагают равным нулю.
По определению  и
и  .
.
Скалярное произведение  называется скалярным квадратом
называется скалярным квадратом  и по определению
и по определению  т. е.
т. е.  =
=  откуда следует
откуда следует  .
.
Из определения следует, что для любых ненулевых векторов  и
и 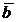 и любого действительного числа μ справедливы соотношения:
и любого действительного числа μ справедливы соотношения:
1.  ·
·  =
=  ·
·  .
.
2. μ·( ·
·  )=(μ
)=(μ  )·
)·  =
=  ·(μ.
·(μ.  ).
).
3.  и, следовательно, ненулевые векторы перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю.
и, следовательно, ненулевые векторы перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю.
Пусть задан вектор  . Если
. Если  ,
,  ,
,  , то числа
, то числа 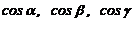 называют направляющими косинусами вектора
называют направляющими косинусами вектора  и координаты вектора
и координаты вектора  представляются в виде:
представляются в виде:

Тогда  и после нормирования вектора получаем
и после нормирования вектора получаем  , т.е. направляющие косинусы вектора
, т.е. направляющие косинусы вектора 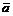 являются координатами его орта
являются координатами его орта  .
.
Если  , то
, то  т.е.
т.е.  . Если в этой формуле орт
. Если в этой формуле орт  0 заменить вектором
0 заменить вектором  , то приходим к понятию проекции вектора на вектор:
, то приходим к понятию проекции вектора на вектор:  , т.е
, т.е  .
.
Воспользуемся этой формулой и докажем линейность скалярного произведения:

Имеем:

что и требовалось доказать.
Пользуясь линейностью скалярного произведения, найдем его для векторов
 = (а1, а2, а3) и
= (а1, а2, а3) и  = (b1, b2, b3)
= (b1, b2, b3)
Для этого сначала запишем координаты вектора  в виде скалярных произведений:
в виде скалярных произведений:  . Затем обе части разложения
. Затем обе части разложения  умножим скалярно на
умножим скалярно на  .
.
Получим:  т.е. скалярное произведение векторов в координатной форме имеет вид:
т.е. скалярное произведение векторов в координатной форме имеет вид:  Из полученной формулы сразу же следует:
Из полученной формулы сразу же следует:
1.  и
и 
2. Если  и векторы
и векторы  и
и  перпендикулярны тогда и только тогда, когда
перпендикулярны тогда и только тогда, когда  .
.
3.  , т.е. сумма квадратов направляющих косинусов одного направления (одного вектора) равна 1.
, т.е. сумма квадратов направляющих косинусов одного направления (одного вектора) равна 1.
4. Если координаты векторов 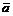 и
и 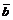 пропорциональны, то векторы коллинеарны, т.к. в этом случае cos(
пропорциональны, то векторы коллинеарны, т.к. в этом случае cos(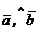 ) =
) =  .
.
Задача 0.38. Используя понятие проекции вектора на вектор, найти длины отрезков, на которые высота BD, опущенная из вершины B (7; 0; 2), делит сторону AC треугольника ABC, если A(-3; 5; -6) и C(3; -4; 12).
 Решение. По координатам точек найдем координаты векторов и вычислим
Решение. По координатам точек найдем координаты векторов и вычислим  .
.


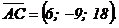

Найдем проекции векторов 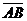 и
и  на вектор
на вектор  .
.
 .
.  .
.
Контроль:  .
.
Ответ:  ,
,  ;
;
Задача 0.39. Радиус–вектор  точки M составляет с осью y угол
точки M составляет с осью y угол  , с осью z угол
, с осью z угол  , а его длина 8. Найдите координаты точки М, если ее абсцисса отрицательна.
, а его длина 8. Найдите координаты точки М, если ее абсцисса отрицательна.
Решение. Координаты вектора  =(x, y, z) выразим через его модуль и направляющие косинусы:
=(x, y, z) выразим через его модуль и направляющие косинусы:  ,
,  ,
,  или
или  ,
,  .
.
Т.к. сумма квадратов направляющих косинусов одного направления равна 1, т.е.  , то
, то  ,
, 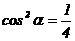 и т. к.
и т. к.  , то
, то  . Следовательно,
. Следовательно,  . Ответ: (-4; 4; 4
. Ответ: (-4; 4; 4  ).
).
Задача 0.40. Вычислить работу, произведенную силой  , если точка ее приложения В(3;-2;-1) переместилась в С(4;-3; 3).
, если точка ее приложения В(3;-2;-1) переместилась в С(4;-3; 3).
Решение. Найдем вектор перемещения точки приложения силы:  . Тогда работа, произведенная силой
. Тогда работа, произведенная силой  , равна по определению скалярному произведению
, равна по определению скалярному произведению  .
.
Ответ: 16 ед. работы.
Задача 0.41. Вектор  перпендикулярен вектору
перпендикулярен вектору  . Скалярное произведение вектора
. Скалярное произведение вектора  и вектора
и вектора  равно 3. Известно, также что
равно 3. Известно, также что  , где
, где  . Найдите координаты вектора
. Найдите координаты вектора  и постройте его в прямоугольной декартовой системе координат.
и постройте его в прямоугольной декартовой системе координат.
 Решение. Если
Решение. Если 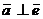 , то
, то  или
или  . Если
. Если  , то
, то  . Если
. Если  , то
, то  или
или  .
.
В итоге решаем систему уравнений.
 Следовательно,
Следовательно,  .
.
На осях x, у и z от начала координат откладываем векторы  ,
,  и
и  и на этих векторах строим параллелепипед, диагональ которого, исходящая из точки О, и является вектором
и на этих векторах строим параллелепипед, диагональ которого, исходящая из точки О, и является вектором  . Ответ:
. Ответ:  .
.
 2017-12-16
2017-12-16 1563
1563
