2017-12-16
584
Пользуясь определением и свойствами векторного произведения, вычислим векторные произведения ортов координатных осей.
Полученной таблицей воспользуемся при вычислении векторного произведения двух произвольных векторов.
Если произведение 
окажется вектором 
, то площадь параллелограмма, построенного на векторах 
и 
с общим началом, вычисляется по формуле 
, а угол φ между векторами и можно найти из соотношения 
.
Воспользуемся выражением векторного произведения через координаты векторов для выяснения геометрического смысла определителя второго порядка.
Пусть на плоскости xy заданы векторы 
Эти же векторы в трехмерном пространстве можно представить в виде: 
Модуль их векторного произведения 
равен модулю определителя 
и равен площади параллелограмма, построенного на векторах 
Понятие векторного произведения имеет свой источник и в механике. А именно, моментом силы 
, приложенной к точке М тела, относительно точки О приложения момента называется вектор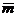 
, равный векторному произведению 
.
Задача 0.44. Вычислить площадь параллелограмма АВDС, если известны три его вершины А(-1; -2), В(1; 3) и С(4; 1).
Решение. Вычислим координаты векторов по координатам их концов. Получим: 
Тогда площадь параллелограмма, построенного на векторах 
равна модулю определителя 
, т.е. равна 19.
Ответ: 19 кв. ед.
Задача 0.45. В(3; –2; 4) – точка приложения силы 
. Найти момент силы 
относительно точки А(2; -1; 1).
Решение. Вычислим координаты вектора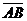 
. Получим: 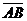= (1; -1; 3). Тогда моментом силы относительно точки А по определению является векторное произведение
= 
Ответ: 
