Если вектор  умножается векторно на вектор
умножается векторно на вектор  и полученный вектор
и полученный вектор  умножается скалярно на вектор
умножается скалярно на вектор  , то тем самым определяется число
, то тем самым определяется число  , называемое векторно–скалярным или смешанным произведением трех векторов
, называемое векторно–скалярным или смешанным произведением трех векторов  ,
,  и
и  , взятых в указанном порядке.
, взятых в указанном порядке.
Геометрический смысл смешанного произведения выражается следующей теоремой.
Модуль смешанного произведения ненулевых и некомпланарных векторов с общим началом равен объему параллелепипеда, построенного на этих векторах.
 Доказательство. Три заданных вектора
Доказательство. Три заданных вектора  ,
, 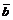 и
и  приведем к общему началу и на них построим параллелепипед.
приведем к общему началу и на них построим параллелепипед.
Скалярное произведение векторов  равно
равно  ,
,
|
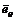 - орт вектора
- орт вектора  Но
Но  - площадь параллелограмма, построенного на векторах
- площадь параллелограмма, построенного на векторах 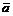 и
и 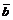 т.е. площадь основания параллелепипеда, а
т.е. площадь основания параллелепипеда, а  - высота параллелепипеда.
- высота параллелепипеда. Следовательно,  SH – объем параллелепипеда.
SH – объем параллелепипеда.
Следствие 1. Если тройка векторов  ,
,  ,
,  правая, то
правая, то  , если левая – то
, если левая – то  .
.
Действительно, если  ,
,  ,
,  - правая тройка векторов, то угол φ между векторами
- правая тройка векторов, то угол φ между векторами  и
и  острый и cos φ > 0. Если же
острый и cos φ > 0. Если же  ,
,  ,
,  - левая тройка векторов, то угол α = π –φ между векторами
- левая тройка векторов, то угол α = π –φ между векторами  и
и  тупой и cos α < 0, а тогда
тупой и cos α < 0, а тогда 
Следствие 2. Т.к.  ,
,  ,
,  и
и  ,
,  ,
,  и
и  ,
,  ,
,  - тройки одной ориентации, то при циклической перестановке векторов их смешанное произведение не изменяется:
- тройки одной ориентации, то при циклической перестановке векторов их смешанное произведение не изменяется: 
Следствие 3. Из коммутативности скалярного произведения 
и из 2-го следствия  получаем
получаем  , т.е. в смешанном произведении знаки скалярного и векторного умножения можно менять местами.
, т.е. в смешанном произведении знаки скалярного и векторного умножения можно менять местами.
В силу следствия 3 смешанное произведение иногда обозначают символом  .
.
Следствие 4. 
Теорема. Смешанное произведение векторов  ,
,  ,
,  равно нулю тогда и только тогда, когда эти векторы компланарны.
равно нулю тогда и только тогда, когда эти векторы компланарны.
Доказательство. Векторы полагаем ненулевыми. В противном случае, если хотя бы один из них нулевой, теорема очевидно верна.
Необходимость. По определению векторного произведения векторы  и
и  перпендикулярны вектору
перпендикулярны вектору  и если (
и если (
 , то и вектор
, то и вектор  перпендикулярен вектору
перпендикулярен вектору  . Но если три вектора
. Но если три вектора  ,
,  и
и  перпендикулярны вектору
перпендикулярны вектору  , то они компланарны.
, то они компланарны.
Достаточность. Если векторы  ,
,  и
и  компланарны, то их можно расположить в одной плоскости a. Вектор
компланарны, то их можно расположить в одной плоскости a. Вектор  перпендикулярен векторам
перпендикулярен векторам 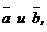 а тогда он перпендикулярен и плоскости a и вектору
а тогда он перпендикулярен и плоскости a и вектору  , поэтому
, поэтому 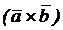
 .
.
Смешанное произведение обладает свойством линейности относительно каждого своего множителя. Например, если полагать  и воспользоваться линейностью скалярного произведения
и воспользоваться линейностью скалярного произведения 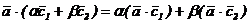 , то получим тождество
, то получим тождество

выражающее линейность смешанного произведения по третьему множителю. Аналогичные тождества справедливы и для первого и для второго множителей, т.к. 
Задача 0.46. Вектор  перпендикулярен векторам
перпендикулярен векторам  . Зная, что
. Зная, что

Решение. Модуль вектора ( ) равен площади параллелограмма, построенного на векторах
) равен площади параллелограмма, построенного на векторах  , т. е. числу
, т. е. числу 
 Векторы
Векторы  и
и  оба перпендикулярны векторам
оба перпендикулярны векторам  и
и  , а потому коллинеарны и косинус угла φ между ними равен -1 либо 1.
, а потому коллинеарны и косинус угла φ между ними равен -1 либо 1.
Следовательно,

Ответ: Если тройка векторов  ,
,  ,
,  правая, то
правая, то 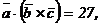 если левая, то
если левая, то  .
.
 2017-12-16
2017-12-16 2293
2293
