2017-12-16
797
Пусть даны две функци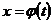и 
и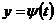 
одной независимой переменной t, определённые и непрерывные в одном и том же промежутке. Если 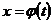строго монотонна, то обратная к ней функция 
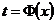однозначна, также непрерывна и строго монотонна. Поэтому у можно рассматривать как функцию, зависящую от переменной х, которая в свою очередь зависит от переменной t, называемой параметром: 
В этом случае говорят, что функция у от х задана параметрически с помощью уравнений 
.
Параметрическое задание функции имеет важное значение при изучении движения точки. Если точка движется на плоскости, то её координаты х,у являются функциями времени t. Задав эти функции 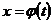, , 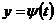мы полностью определим движение точки. Для каждого промежутка времени в котором функция 
строго монотонна, можно определить функцию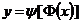 
, графиком которой является кривая, описываемая за этот промежуток времени движущейся точкой, т.е. траектория движения.
