2017-12-16
1109
Предположим, что функци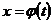и 
и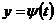 
имеют производные, причём 
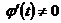на некотором промежутке. Отсюда вытекает строгая монотонность функции 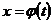и, следовательно, однозначность обратной функции 
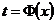. По теореме о производной обратной функции, функция 
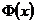имеет производную 
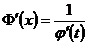, а функция 
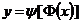по теореме о производной сложной функции имеет производную 
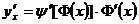. Следовательно 
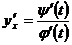или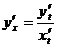 
.
Выведенная формула даёт возможность находить производную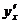 
от функции, заданной параметрически, не находя выражения непосредственной зависимости у от х.
Пример. Пусть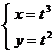 
Найти .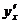
Решение: имеем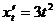 
, 
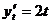, следовательно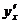 
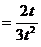, т.е.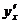 
.
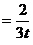В этом можно убедиться, найдя непосредственно зависимость у от х. Действительно,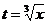 
. Тогда 
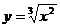. Отсюда 
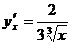, т.е. .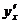
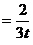Если функция задана в неявном виде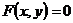 
, то для нахождения производной от у по х нет необходимости разрешать уравнение относительно у: достаточно продифференцировать это уравнение по х, рассматривая при этом у как функцию х, и полученное затем уравнение разрешить относительно 
.
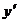Производная неявной функции выражается через аргумент х и функцию у.
Пример. Найти производную функции, заданную уравнением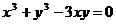 
.
Решение. Функция у задана неявно. Дифференцируем по х равенство
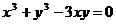. Из полученного соотношения
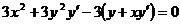
следует, что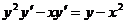 
, т.е. 
.
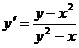Заключение.
Формулы и правила дифференцирования суммы, разности, произведения, частного и правило дифференцирования сложной функции являются основными формулами дифференциального исчисления. На основе правил и формул дифференцирования можно сделать важный вывод: производная любой элементарной функции также элементарная функция. Таким образом, операция дифференцирования не выводит из класса элементарных функций.
