Определение производной, её геометрический смысл

Производная функции.

1. Определение производной, её геометрический смысл.

2.Производная сложной функции.

3. Производная обратной функции.

4. Производные высших порядков.

5. Параметрически заданные функции и неявно.

6. Дифференцирование функций, заданных параметрически и неявно.

Введение.

Источником дифференциального исчисления были два вопроса, выдвинутые запросами науки и техники в 17 веке.

1) Вопрос о вычислении скорости при произвольно заданном законе движения.

2) Вопрос о нахождении (с помощью вычислений) касательной к кривой произвольно заданной.

Задачу проведения касательной к некоторым кривым решил ещё древнегреческий учёный Архимед (287-212 г.г. до н.э.), пользуясь методом вычерчивания.

Но только в 17 и 18 веках в связи с прогрессом естествознания и техники эти вопросы получили должное развитие.

Одним из важных вопросов при изучении любого физического явления обычно является вопрос о скорости, быстроте происходящего явления.

Скорость с которой движется самолёт или автомобиль, всегда служит важнейшим показателем его работы. Быстрота прироста населения того или иного государства является одной из основных характеристик его общественного развития.

Первоначальная идея скорости ясна каждому. Однако для решения большинства практических задач этой общей идеи недостаточно. Необходимо иметь такое количественное определение этой величины, которую мы называем скоростью. Потребность в таком точном количественном определении исторически послужила одним из основных побудителей к созданию математического анализаю. Целый раздел математического анализа посвящен решению этой основной задачи и выводам из этого решения. К изучению этого раздела мы и переходим.

Определение производной, её геометрический смысл.

Пусть дана функция 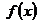определённая в некотором интервале (а,в) и непрерывная в нём.

1. Дадим аргументу х приращение , тогда функция получит

приращение :

= -

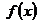
2. Составим отношение .

3. Переходя к пределу в при и, предполагая, что предел

существует, получим величину , которую называют

производной функции 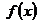по аргументу х.

Определение. Производной функции 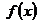в точке называется предел отношения приращения функции к приращению аргумента , когда →0.

Значение производной очевидно зависит от точки х, в которой оно найдено, поэтому производная функции 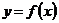есть в свою очередь некоторая функция от х. Обозначается .

По определению имеем

или (3)

Пример. Найти производную функции .

1. ;

2.

3.

4. . Итак .

Механический смысл производной:

скорость прямолинейного движения материальной точки в момент времени t₀ есть производная пути по времени

Геометрический смысл производной:

тангенс угла наклона касательной к графику функции y=f(x) в точке с абсциссой x₀ равен производной функции f(x) в точке x₀

Уравнение касательной к кривой: (4)

Нормаль к кривой в точке М₀ – прямая проходящая через точку М₀, перпендикулярно касательной к кривой в этой точке.

Уравнение нормали к кривой: . (5)