Пусть у=f (x) является дифференцируемой в каждой точке интервала (a; b). Тогда в каждой точке этого интервала существует функция  – производная от данной (ее называют также первой производной или производной первого порядка функции f (x)). Может случиться, что она так же имеет производную. Тогда эта производная называется второй производной или производной второго порядка функции f (x) и обозначается следующим образом:
– производная от данной (ее называют также первой производной или производной первого порядка функции f (x)). Может случиться, что она так же имеет производную. Тогда эта производная называется второй производной или производной второго порядка функции f (x) и обозначается следующим образом:
 .
.
Подобным образом определяются третья, четвертая и все последующие производные:
 .
.
Определение 3.3.1. Производная от производной порядка n –1 называется производной порядка n и обозначается
 .
.
Аналогично вводится понятие дифференциала n-го порядка.
Определение 3.3.2. Дифференциалом n-го порядка называется дифференциал от дифференциала (n – 1)-го порядка и обозначается:
 .
.
Говорят: дифференциал n -го порядка равен произведению производной n -го порядка на n -ную степень дифференциала независимой переменной.
Отсюда имеем:  .
.
Пример 3.3.1. Для у=sinx получим


 и так далее;
и так далее;
 ,
,  ,
,  и так далее.
и так далее.
Приложения производной
 3.4.1. Геометрический и физический смысл производной и дифференциала
3.4.1. Геометрический и физический смысл производной и дифференциала
Геометрический смысл производной тесно связан с понятием касательной.
Рассмотрим непрерывную кривую Г – график непрерывной на заданном интервале функции у=f (x) (рис. 3.17). Пусть М(х; у) – лежащая на ней точка и М1( ),
),  – другая, лежащая на Г точка. Прямую S, проходящую через М и М1 называют секущей (кривой Г). Если теперь точку М1 двигать непрерывно по Г, неограниченно приближая к М, тогда секущая S будет вращаться относительно М. Может случиться, что при этом S будет стремиться занять в пределе положение вполне определенной (проходящей через М) прямой. В этом случае говорят, что кривая Г имеет в точке M касательную (на рис. 3.17 – прямая Т). Уравнение касательной к графику функции f (x) в точке М0(х 0; у 0) имеет вид:
– другая, лежащая на Г точка. Прямую S, проходящую через М и М1 называют секущей (кривой Г). Если теперь точку М1 двигать непрерывно по Г, неограниченно приближая к М, тогда секущая S будет вращаться относительно М. Может случиться, что при этом S будет стремиться занять в пределе положение вполне определенной (проходящей через М) прямой. В этом случае говорят, что кривая Г имеет в точке M касательную (на рис. 3.17 – прямая Т). Уравнение касательной к графику функции f (x) в точке М0(х 0; у 0) имеет вид:
 .
.
Секущая S, проходящая через точки М и М1, образует с положительным направлением оси О х угол  (рис. 3.17), тангенс которого
(рис. 3.17), тангенс которого  (
( – отношение противолежащего катета к прилежащему в прямоугольном треугольнике
– отношение противолежащего катета к прилежащему в прямоугольном треугольнике  ).
).
Из того, что угол между секущей и касательной при стремлении точки М1 к точке М, т.е. при уменьшении  х до нуля, стремится к нулю, вытекает, что угол
х до нуля, стремится к нулю, вытекает, что угол  перейдет в угол a наклона касательной к оси О х (рис. 3.17). Тогда получаем
перейдет в угол a наклона касательной к оси О х (рис. 3.17). Тогда получаем
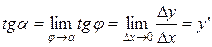
Следовательно, производная функции в точке равна 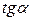 – угловому коэффициенту касательной, проведенной к графику функции в этой точке.
– угловому коэффициенту касательной, проведенной к графику функции в этой точке.
Подчеркнем, что в уравнении касательной к графику функции f (x) в точке М0(х 0; у 0) также  – производная функции в этой точке равна угловому коэффициенту касательной, проведенной к графику функции в точке М0(х 0; у 0).
– производная функции в этой точке равна угловому коэффициенту касательной, проведенной к графику функции в точке М0(х 0; у 0).
Подчеркнем, что уравнение нормали к графику функции f (x) в точке М0(х 0; у 0) имеет вид:

 Геометрический смысл дифференциала.
Геометрический смысл дифференциала.
Дифференциалом функции у=f (х) первого порядка называется главная, линейная относительно приращения 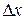 , часть приращения функции
, часть приращения функции 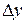 , равная произведению производной этой функции на приращение аргумента
, равная произведению производной этой функции на приращение аргумента  х, обозначаемое в этом случае, как dx:
х, обозначаемое в этом случае, как dx:
dy =  = tga dx
= tga dx
Физический смысл производной.
Пусть точка движется прямолинейно по закону s = f (t).
Средняя скорость точки за промежуток времени от t до  равна отношению пути
равна отношению пути  , пройденного за этот промежуток времени ко времени движения
, пройденного за этот промежуток времени ко времени движения 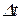 :
:
 .
.
Тогда число v, к которому стремиться средняя скорость точки, движущейся прямолинейно по закону s = f (t), на промежутке времени [ t,  ] при
] при  , есть ее скорость или мгновенная скорость в момент времени t:
, есть ее скорость или мгновенная скорость в момент времени t:
 .
.
Физический смысл второй производной.
Рассматривая производную скорости по времени t, получим скорость изменения скорости, то есть ускорение.
Таким образом, вторая производная от пути по времени есть ускорение а прямолинейно движущейся точки в момент времени t:  .
.
3.4.2. Основные теоремы о дифференцируемых функциях и их приложения
Теорема 3.4.1. Если функция f (х) дифференцируема в точке х 0, то она непрерывна в этой точке.
Утверждение, обратное теореме 3.4.1., вообще говоря, неверно – существуют функции, непрерывные в некоторой точке, но не дифференцируемые в ней. Рассмотрим пример.
Пример 3.4.1. Хорошо известно, что функция | x | непрерывна при всех значениях x (см. пример 3.1.7.). Докажем, что она не является дифференцируемой при х =0.
○Так как f (x)=| х |, f (x +Δ х)=| х +Δ х |, то Δ f =| х +Δ х |–| х | и при х =0 имеем Δ f =|Δ х |. Поэтому

 Так как пределы
Так как пределы 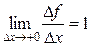 и
и  различны, то не существует предела
различны, то не существует предела  , и потому функция | х | не является дифференцируемой в точке х =0.
, и потому функция | х | не является дифференцируемой в точке х =0.
Наглядный смысл того, что функция | х | не имеет производной в точке х =0, состоит в том, что график этой функции имеет излом в начале координат (рис. 3.19). Геометрический смысл недифференцируемости функции | х | в точке х =0 – неопределенность касательной к ее графику в этой точке: множество прямых, проходящих через точку О(0; 0), имеют единственную общую точку с графиком данной функции, и, значит, каждая из них является касательной.●
Теорема 3.4.2. (Теорема Ферма). Если функция у = f (х), определенная на интервале (a; b), достигает в некоторой точке с этого интервала наибольшего (или наименьшего) значения и существует производная f¢ (с), то f¢ (с)=0.
Геометрический смысл заключения теоремы состоит в том, что касательная к графику функции у = f (х) в точке с абсциссой с параллельна оси Ox.
Теорема 3.4.3. (Теорема Ролля). Пусть функция f (х) непрерывна на отрезке [ a; b ], имеет производную на интервале (a; b) и принимает равные значения на концах отрезка [ a; b ] (f (a)= f (b)). Тогда на интервале (a; b) всегда найдется такая точка с, что в ней производная от f (х) равна нулю:
 .
.
Эта теорема, по существу утверждает, что при некоторых дополнительных условиях между двумя «нулями» функции всегда лежит «нуль» ее производной.
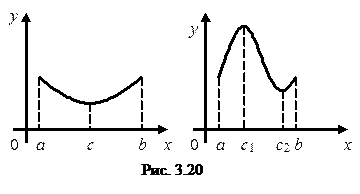 На рисунке 3.20 изображены графики функций, удовлетворяющих условию теоремы Ролля. У первой функции имеется одна точка из интервала (a; b), в которой ее производная равна нулю (
На рисунке 3.20 изображены графики функций, удовлетворяющих условию теоремы Ролля. У первой функции имеется одна точка из интервала (a; b), в которой ее производная равна нулю ( ), у второй имеются две такие точки с 1 и с 2 (
), у второй имеются две такие точки с 1 и с 2 ( ).
).
Прозрачен геометрический смысл теоремы Роля: если функция имеет равные значения на концах отрезка и дифференцируема на соответствующем интервале, то найдется точка с этого интервала, в которой касательная к графику функции параллельна оси абсцисс.
Теорема 3.4.4. (Теорема Лагранжа) Пусть функция f (х) непрерывна на отрезке [ a; b ] и имеет производную на интервале (a; b). Тогда на интервале (a; b) найдется точка с такая, что в ней производная от f (х) удовлетворяет равенству

или, что то же самое, равенству
 .
.
Теорема Лагранжа имеет следующий геометрический смысл.
Левая часть первого равенства из теоремы 3.4.4. представляет собой тангенс угла наклона к оси О х хорды, стягивающей точки (a; f (a)) и (b; f (b)) графика функции у = f (х), а правая часть – тангенс угла наклона касательной к графику в некоторой точке с, принадлежащей (a; b).
Теорема Лагранжа утверждает, что если кривая есть график непрерывной на [ a; b ] функции, имеющей производную на (a; b), то на этой кривой существует точка, соответствующая некоторой абсциссе с (a < c < b), такая, что касательная к кривой в этой точке параллельна хорде, стягивающей концы кривой (a; f (a)) и (b; f (b)) (рис. 3.21).
 Лемма 3.4.1. Если функция у = f (х) непрерывна на отрезке [ a; b ], то ее производная равна нулю во всех внутренних точках отрезка тогда и только тогда, когда функция у = f (х) постоянна на этом отрезке.
Лемма 3.4.1. Если функция у = f (х) непрерывна на отрезке [ a; b ], то ее производная равна нулю во всех внутренних точках отрезка тогда и только тогда, когда функция у = f (х) постоянна на этом отрезке.
Правило Лопиталя
Теорема 3.4.4. (Правило Лопиталя). Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных, если последний существует, то есть
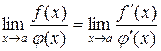 .
.
Правило Лопиталя используется для раскрытия неопределенностей вида отношения 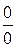 или
или  , а также приводимых к ним
, а также приводимых к ним  и некоторых других. Для этого отношение функций заменяется отношением их производных до тех пор, пока неопределенность не исчезнет:
и некоторых других. Для этого отношение функций заменяется отношением их производных до тех пор, пока неопределенность не исчезнет:
 .
.
Примечание. При отсутствии неопределенности вида 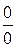 или
или  правило Лопиталя применять нельзя.
правило Лопиталя применять нельзя.
Пример 3.4.2. Вычислим  .
.
○Здесь имеем неопределенность вида 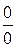 . Воспользовавшись правилом Лопиталя, можем записать:
. Воспользовавшись правилом Лопиталя, можем записать:
 .●
.●
Неопределенности вида  или
или 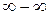 приводятся к виду
приводятся к виду 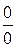 или
или  . Обычно это достигается с помощью элементарных преобразований заданного выражения.
. Обычно это достигается с помощью элементарных преобразований заданного выражения.
Так для раскрытия неопределенностей вида  используют следующий прием. От произведения f (x) g (x), где
используют следующий прием. От произведения f (x) g (x), где  ,
,  легко перейти к дробям
легко перейти к дробям  (получим неопределенность вида
(получим неопределенность вида 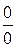 ) или
) или  (неопределенность вида
(неопределенность вида  ) и использовать правило Лопиталя обычным образом.
) и использовать правило Лопиталя обычным образом.
Пример 3.4.3. Вычислим  .
.
○Здесь имеем неопределенность вида  . Чтобы свести ее к виду
. Чтобы свести ее к виду 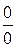 , представим произведение в виде дроби:
, представим произведение в виде дроби:

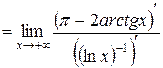



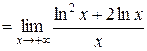 =
= 
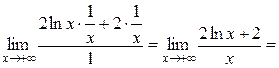

 .●
.●
Пример 3.4.4. Вычислим  .
.
○ 


 .●
.●
Рассмотрим способ раскрытия неопределенности вида 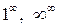 и т.п.
и т.п.
Функции вида  удобно сначала прологарифмировать. Если у =
удобно сначала прологарифмировать. Если у =  , то
, то  . Полученное произведение приводим к отношению
. Полученное произведение приводим к отношению  или
или  , после чего для вычисления соответствующего предела можно применять правило Лопиталя. В итоге получим
, после чего для вычисления соответствующего предела можно применять правило Лопиталя. В итоге получим  , где А – некоторое число, откуда, потенцируя, будем иметь
, где А – некоторое число, откуда, потенцируя, будем иметь  .
.
Пример 3.4.5. Вычислим  .
.
○Найдем предел логарифма данной функции.


 .
.
Значит,  .●
.●
 2017-10-31
2017-10-31 1062
1062
