2017-10-31
446
В современных условиях построение графиков осуществляется на практике, как правило, по точкам или с помощью компьютера. В многочисленных исследованиях необходимо более детальное изучение поведения функции. Для этого используются описанные выше приемы. Схема анализа функции и построения ее графика состоит из следующих этапов:
1. Находится область определения функции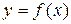 
.
2. Устанавливается не является ли функция четной или нечетной.
3. Выясняется, не является ли функция периодической.
4. Функция исследуется на непрерывность, в случае, если функция не является непрерывной находятся точки разрыва.
5. Исследуется поведение функции в граничных точках области определения, находятся асимптоты.
6. Находятся точки пересечения графика функции с осями координат x =0, y =0; промежутки знакопостоянства (то есть, находим промежутки, на которых f (x)>0, f (x)<0).
7. Находятся стационарные точки. Определяются экстремумы и интервалы монотонности функции.
8. Определяются интервалы выпуклости и точки перегиба графика функции.
9. Находятся значения функции в нескольких дополнительных точках.
Исследование функции проводится одновременно с построением графиков.
Пример 3.4.6. Исследовать функцию 
и построить ее график.
○
1. Областью определения функции является множество действительных чисел.
2. Исследуем функцию на четность и нечетность.
.
Функция является четной, так как 
, и она определена на интервале (–∞; +∞), симметричном относительно начала координат.
3. Функция не является периодической, так как для любого х не выполняется условие f (x + Т)= f (x)= f (x – T).
4. Функция непрерывна на R как элементарная.
5. Функция не имеет вертикальных асимптот, так как она непрерывна на R и для любого х 0ÎR 
R.
Так как 
, то нет горизонтальных асимптот.
Поскольку 
, то и наклонных асимптот нет.
6. Найдем нули функции:
.
Корни разбивают область определения функции на интервалы: (–∞; 
), (; 0), (0; 
), (; +∞).
y (x)>0 на интервалах (; 0), (0; ) и y (x)<0 на интервалах (–∞; ), (; +∞).
7. Найдем стационарные точки:
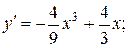
Последнее уравнение имеет корни: 
.
Корни разделяют множество действительных чисел на четыре интервала:
| x | (–∞;  )
|
| (; 0)
| (0;  )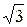
|
| (; +∞)
| |
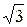
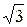| y' | + | – | + | – | |||
| y | 
| 
| 
| 
| |||
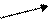
| max | min | max |
8. Найдем 
Составим таблицу:
| x | (–∞;–1) | –1 | (–1; 1) | (1; +∞) | |
| y'' | – | + | – | ||
| y | 
| 
| 
|
|
|
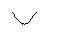
9.
| x | ±1 | ±2 | ±2,7 |
| y | »0,56 | »0,89 | »–1,04 |
График функции имеет вид:
Рис. 3.26
●
