Понятие дифференциала

Согласно теореме 3.1.1 функцию 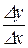можно представить в виде , откуда . Так как – бесконечно малая и стремится к нулю, то вторым слагаемым можно пренебречь. Слагаемое называют дифференциалом функции у=f (х) и обозначают или .

Определение 3.2.3. Дифференциал функции равен произведению ее производной на приращение аргумента:

.

Рассмотрим функцию f (х)= х. Так как , то . Таким образом, считают, что дифференциал аргумента равен его приращению: . Имеем

,

откуда .

Запись (или ) используется для обозначения производной функции у=f (х).

Пример 4.2.2. Найти дифференциал функции .

○ .●

Правила дифференцирования функций