2018-01-08
803
Рассмотрим сложение двух гармонических колебаний одинакового направления и частоты, которые происходят с некоторой разностью фаз и имеют разные амплитуды. Смещение x1 от положения равновесия колеблющегося тела будет равно сумме смещений x1 и x2:
= 
,
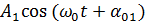, (15)
Построим векторные диаграммы колебаний (15).
С
1
О 
X2 x
X1
X
Рисунок 2 – Сложение колебаний и 
с помощью векторного метода
Поскольку вектор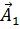 
в начальный момент времени располагается под углом 
к оси x, а вектор 
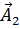– под углом 
, то в результате сложения оба вектора будут вращаться против часовой стрелки с одинаковой угловой скоростью 
. Получаем, что угол между векторам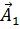и и 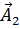все время остается постоянным и равным 
По правилам сложения векторов построим суммарный вектор . Вектор представляет суммарное колебание. Он вращается с той же угловой скоростью , что и векторы 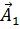и 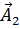. Проекция этого вектора на ось X равна сумме проекций слагаемых векторов: x= х1+х2.
Приходим к выводу, что результирующее движение будет гармоническим колебанием с частотой ω0, амплитудой A и начальной фазой α.
. (16)
Выразим с уравнения (16) амплитуду А
(17)
Амплитуда A результирующего колебания зависит от разности начальных фаз α02−α01 слагаемых колебаний. Получаем, что разность α02−α01 с течением времени не изменяется (такие синхронные колебания называются когерентными), по формуле (17) можно получить значения амплитуды A. Поскольку косинус любого угла не может быть больше +1 и меньше –1,то возможные значения амплитуды заключены в пределах:
A1+A2≥ A ≥ ǀA2−A1 ǀ.
