2018-01-08
997
Рассмотрим уравнения, которые имеют вид
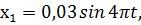(33)
Построим график уравнений (33). Для этого составим таблицу значений 
.
Таблица 2
Зависимость смещения материальной точки в плоскости по координатам х1 и х2 от времени, 
| t,c | X1,м | Х2,м | x,м |
| 0,05 | 0,017626 | 0,06 | 0,077626 |
| 0,1 | 0,028526 | 9,56E-05 | 0,028621 |
| 0,15 | 0,028541 | -0,06 | -0,03146 |
| 0,2 | 0,017664 | -0,00019 | 0,017473 |
| 0,25 | 4,78E-05 | 0,06 | 0,060047 |
| 0,3 | -0,01759 | 0,000287 | -0,0173 |
| 0,35 | -0,02851 | -0,06 | -0,08851 |
| 0,4 | -0,02856 | -0,00038 | -0,02894 |
| 0,45 | -0,0177 | 0,059998 | 0,042295 |
| 0,5 | -9,6E-05 | 0,000478 | 0,000382 |
| 0,55 | 0,017548 | -0,06 | -0,04245 |
| 0,6 | 0,028496 | -0,00057 | 0,027923 |
| 0,65 | 0,02857 | 0,059997 | 0,088567 |
| 0,7 | 0,017742 | 0,000669 | 0,018411 |
Рисунок 8 – Зависимость смещения от времени: 
Рисунок 9 – Зависимость результирующего колебания смещения от времени
Из уравнений колебания (33),найдем амплитуду и частоту каждого из них
А1=0,03 (м), ν1=2 (Гц), А2= 0,06 (м), ν2=5 (Гц). (34)
По данным (34) начертим спектр результирующего колебания
А, м
0,06
0,04
0,02
ν, Гц
1 2 3 4 5
Рисунок 10 – Cпектр результирующего колебания
Каждый спектр, представляющий собой монохроматическое колебание входит в спектр не только со своей определенной частотой, но и с амплитудой, и фазой.
