Сложение двух гармонических колебаний одного направление с разными частотами

Рассмотрим случай, когда два скла­дываемых гармонических колебания одинакового на­правления мало отличаются по частоте. Как мы сейчас покажем, результирующее движение при этих условиях можно рассматривать гармоническое колебание с пульсирующей амплитудой. Такое колебание называется биениями.

Обозначим частоту одного из колебаний буквой , частоту второго колебания через 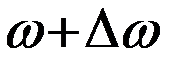. По условию 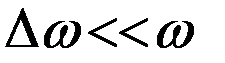. Амплитуды обоих колебаний будем полагать одинаковыми и равными . Поскольку частоты колеба­ний несколько отличны, всегда можно выбрать начало отсчета времени так, чтобы начальные фазы обоих ко­лебаний были равны нулю.

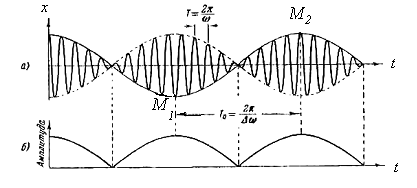
Рисунок 4 - Биения и их переменная амплитуда

Практически это означает, что мы должны дождаться, пока смещения в обоих колебаниях достигнут одновременно наибольшего положительного значения, и в этот момент «запустить секундомер». Тогда уравнения обоих колебаний будут иметь следующий вид:

(t) = Аcosωt,

(t) = Аcos(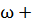 ∆ω)(18)

Складывая выражения (18) и применяя тригоно­метрическую формулу для суммы косинусов, получаем:

х(t) = 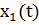+ 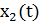= (2Аcos 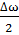t) cosωt.(19)

(во втором множителе пренебрегаем членом 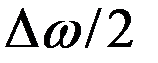по сравнению с ).

А, м

A₂

A₁

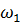
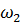ω,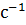

Рисунок 5 - Спектр А(ω) биений

Заключенный в скобки множитель в формуле (19) изменяется гораздо медленнее, чем второй множитель. Ввиду условия 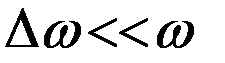за то время, за которое множи­тель 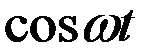совершает несколько полных колебаний, мно­житель, стоящий в скобках, почти не изменится. Это дает нам основание рассматривать колебание (19) как гармоническое колебание частоты , амплитуда ко­торого изменяется по некоторому периодическому за­кону. Выражением этого закона не может быть множи­тель, стоящий в скобках, так как он изменяется в пределах от -2 а до +2 а, в то время как амплитуда по оп­ределению — положитель­ная величина. График ам­плитуды показан на рис. 3,б. Аналитическое выра­жение амплитуды, очевидно, имеет вид:

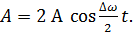(20)

Функция (20) — перио­дическая функция с часто­той, в 2 раза превышающей частоту выражения, стоящего под знаком модуля, т. е. с частотой 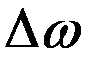. Получаем, частота пульсаций амплитуды — ее называют частотой биений — равна разности частот складываемых колебаний.

Отметим, что множитель 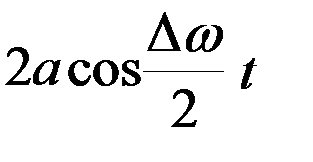не только опре­деляет амплитуду, но и влияет на фазу колебания. Это проявляется, например, в том, что отклонения, соот­ветствующие соседним максимумам амплитуды, имеют противоположные знаки.