2018-01-08
537
Рассмотрим выражение
(6)
преобразуем выражение (5) следующим образам:
х(t) = 
(
(7)
Выражение (6),преобразование называется метод вспомогательного угла.
Заметим, что
,
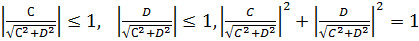Тогда по своим свойствам эти дроби напоминают синус и косинуса угла. Поэтому введем обозначения
, 
(8)
Выражение (6) можно переписать в виде
х(t)= 
(
(9)
Полученное выражение (8) вместе с (6) дает еще одну форму представления гармонического колебания. Смысл коэффициентов С и D в формуле (6) легко устанавливается из начального условия.
Начальное условие – это значение физической величины в момент времени (t = 0), и значение ее скорости изменений t = 0.
,
где 
—начальные условия.
Замечание по формуле (8): мы могли принять за sin 
первое выражение, а за cos второе выражение. При этом в конечной формуле (9) функция косинус заменилась бы на формулу sin 
перед 
стояло бы значение t. Поскольку в физике и технике значение фазы имеет принципиальное значение, то в одной и той же задачи следует использовать одну из функций либо синус, либо косинус.
|
|
|
, 
(10)
Тогда введем дополнительный угол по формуле (10), получим
(11)
Из формулы (10) следует, что результатом сложения одночастотных и однонаправленных колебаний являются колебания той же частоты 
,что и складываемая, то есть с другой амплитудой и фазой.
