В зависимости от количества факторов, включенных в уравнение регрессии, различают парную и множественную регрессии.
Уравнение взаимосвязи двух переменных и x называют парной регрессией, а зависимость y от нескольких объясняющих переменных 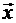 = (x 1, x 2, ... xn)– множественной регрессией.
= (x 1, x 2, ... xn)– множественной регрессией.
Уравнение парной регрессии имеет вид:
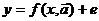
где 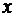 - независимая переменная, влияющая на у;
- независимая переменная, влияющая на у; 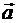 – коэффициенты модели.
– коэффициенты модели.
Как уже отмечалось, на первом этапе эконометрического исследования проводится выбор формы взаимосвязи переменных, т.е. осуществляется спецификация уравнения регрессии. С этой целью их круга факторов, влияющих на результирующую переменную у, выделяются наиболее существенно влияющие факторы. Парная регрессия считается достаточной, если можно выделить доминирующий фактор, который используется в качестве объясняющей (независимой) переменной. От правильности выбора спецификации модели зависит величина случайных ошибок: они тем меньше, чем ближе фактические данные у к рассчитанным по построенному уравнению значениям 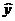 .
.
К ошибкам спецификации модели относится не только неправильный выбор той или иной математической функции f взаимосвязи переменных у и 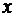 , но недоучет в уравнении регрессии какого-либо существенного фактора, т.е. использование парной регрессии вместо множественной.
, но недоучет в уравнении регрессии какого-либо существенного фактора, т.е. использование парной регрессии вместо множественной.
В парной регрессии выбор математической функции 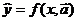 можно осуществить графически, аналитически и экспериментальным путем.
можно осуществить графически, аналитически и экспериментальным путем.
Чаще всего для подбора вида уравнения парной регрессии используется графический метод, основанный на построении поля корреляции. Основные типы кривых, используемых при оценке взаимосвязей переменных, представлены на рисунке 1:
 |

а) 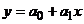 б)
б) 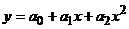 в)
в) 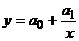

г) 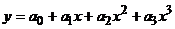 д)
д) 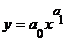 е)
е) 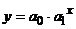
Аналитический метод выбора типа уравнения регрессии состоит в изучении материальной природы взаимосвязи исследуемых факторов и учете степеней их влияния друг на друга в уравнении регрессии.
При использовании экспериментального метода строятся уравнения различных типов, а затем из них выбирается наилучшее с точки зрения величины дисперсии ошибки:
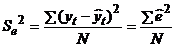 .
.
Чем меньше величина дисперсии ошибки, тем лучше построенное уравнение регрессии подходит к исходным данным.
 2018-01-08
2018-01-08 1573
1573