Определители, их основные свойства и вычисление

Минором элемента называется определитель (n-1) порядка, полученный из исходного определителя удалением i-строки и j-столбца

Алгебраическим дополнением элемента называется минор

Следствие из теоремы Лапласа - определитель равен сумме произведений элементов какой-либо строки(столбца), умноженных на их алгебраическое дополнение.

Свойства определителя:

1. Если строки или столбцы поменять местами, то его величина не изменится

Это свойство определяет, что строки и столбцы определителя равноправны

(Операция замены строк столбцами с сохранением нумерации называется транспонированием)

2. Если все элементы строки(столбца) определителя равны нулю, то и сам определитель равен нулю.

3. Если в определителе элементы строки(столбца) имеют общий множитель, то его можно вынести за знак определителя

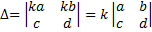
4. Если определитель имеет две одинаковые строки(столбца), то он равен нулю.

5. Если в определителе переставить местами две строки(столбца), то определитель изменит знак на противоположный

6. Если в определителе строки(столбцы) пропорциональны элементам другой строки(столбца), то определитель равен нулю

7. Если все элементы строки или столбца представлены в виде суммы двух слагаемых, то такой определитель можно представить в виде суммы двух определителей

8. Если к элементам некоторой строки или столбца прибавить соответствующие элементы другой строки или столбца, умноженных на любой множитель k, то величина определителя не изменится