2018-01-08
663
Основные приложения скалярного произведения
1) Вычисление работы (A), силы (F), затраченной на перемещение из точки B точку C
2) Вычисление угла между векторами
3) Вычисление проекции одного вектора на другой
Векторное произведение векторов, его основные свойства, геометрический и механический смысл.
Векторным произведением 
называется вектор 
, удовлетворяющий условиям:
1) 
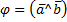
2) 
3) 
Свойства векторного произведения:
1) Антикоммутативность
2) Ассоциативность относительно числового множителя
3) Дистрибутивность
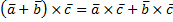
4) Условие коллинеарных векторов
Ненулевые векторы коллинеарны тогда и только тогда, когда их векторное произведение равно нулю
; (
)
Геометрический смысл векторного произведения:
Модуль векторного произведения численно равен площади параллелограмма, построенного на этих векторах как на сторонах.
Механический смысл векторного произведения:
Если вектор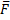 
- сила, а вектор 
- есть радиус-вектор точки приложения силы, имеющий своё начало в точке O, то момент силы 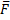относительно точки O, 
- есть вектор, равный векторному произведению радиус -вектора (точки приложения силы) на силу 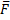, то есть:
|
|
|
