Базис, разложение вектора по базису, координаты вектора, линейные операции над векторами в координатах

Базис - максимальная линейно независимая система векторов.

(максимальная система - система, при добавлении в которую одного вектора, система становится линейно зависимая)

Базисом на плоскости называются два неколлинеарных вектора, а в пространстве три некомпланарных.

- базис

- произвольный вектор

Коэффициенты разложения - координаты вектора в базисе

Линейные операции над векторами:

Пусть в базисе заданы векторы и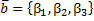

1) Сложение и вычитание

2) Умножение вектора на число

,

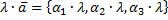Если векторы и 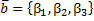коллинеарны, то их соответствующие векторы пропорциональны:

Скалярное произведение векторов, его основные свойства, условия параллельности и перпендикулярности.

Скалярным произведением двух векторов называется число, равное произведению этих векторов на косинус угла между ними:

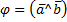
Свойства скалярного произведения:

1) Коммутативность

2) Ассоциативность

3) Дистрибутивность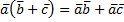

4) скалярное произведение двух векторов равно длине одного из векторов, умноженного на проекцию другого вектора = =

5) Скалярный квадрат вектора равен квадрату его длины

6) Для того, чтобы два ненулевых вектора были взаимно перпендикулярны, необходимо и достаточно, чтобы их скалярное произведение равнялось нулю

Таким образом:

Выражение скалярного произведения векторов через координаты сомножителей.

Пусть

A(, B()