Системы линейных алгебраических уравнений, формулы Крамера

Рассмотрим систему линейных уравнений третьего порядка:

Запишем определитель системы, то есть определитель, состоящий из коэффициентов при переменных:

Пусть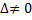

Составим определители, заменяя в определителе системы столбец коэффициентов при выбранной переменной столбцом, состоящим из свободных членов:

,

Если определитель системы отличен от нуля, то системы линейных уравнений имеют единственное решение, которое определяется формулами

,

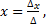
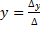Таким образом,

•если определитель системы отличен от нуля, то система совместная определенная (имеет 1 решение)

•если определитель равен нулю, то возможны два случая:

а) если хотя бы один определитель , то система несовместна (решений нет)

б) если все определители 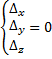, система совместная неопределенная (бесконечное множество решений)

3. Определение вектора, модуль вектора, коллинеарные и компланарные векторы, равенство векторов.

Вектором называется направленный отрезок, то есть отрезок, с указанными начальной и конечной точками

Модулем (длиной) вектора называется длина отрезка АВ -

Векторы, лежащие на одной прямой или на параллельных прямых, называются коллинеарными

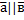
Коллинеарные векторы могут быть сонаправлены 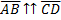или

противоположнонаправлены

Векторы, лежащие в одной плоскости или в параллельных плоскостях, называются компланарными

Два вектора называются равными, если они компланарны, коллинеарны и их длины равны