Будем рассматривать dx в выражении для dy как постоянный множитель. Тогда функция dy представляет собой функцию только аргумента x и ее дифференциал в точке x имеет вид (при рассмотрении дифференциала от dy будем использовать новые обозначения для дифференциалов): δ (d y) = δ [ f ' (x) d x ] = [ f ' (x) d x ] ' δ x = f '' (x) d (x) δ x.
Дифференциал δ (d y) от дифференциала dy в точке x, взятый при δ x = dx, называется дифференциалом второго порядка функции f (x) в точке x и обозначается d 2 y, т.е.
d 2 y = f ''(x)·(dx)2.
В свою очередь, дифференциал δ(d 2 y) от дифференциала d 2 y, взятый при δ x = dx, называется дифференциалом третьего порядка функции f (x) и обозначается d 3 y и т.д.
Дифференциал δ(d n-1y) от дифференциала dn -1 f, взятый при δ x = dx, называется дифференциалом n - го порядка (или n - м дифференциалом) функции f (x) и обозначается dny.
Механический смысл второй производной:
Так как производная от координаты есть скорость, то, в свою очередь, производная от скорости есть ускорение: 
Основные теоремы дифференциального исчисления: теорема Роля, теорема Лагранжа, теорема Коши.
|
|
|
Т.Роля:
Если 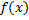 непрерывна на отрезке
непрерывна на отрезке  , дифференцируема в интервале (a;b) и принимает на отрезках AB равные значения => внутри AB существует по крайней мере одна точка C, в которой производная обращается в ноль.
, дифференцируема в интервале (a;b) и принимает на отрезках AB равные значения => внутри AB существует по крайней мере одна точка C, в которой производная обращается в ноль.



Т.Лагранжа:

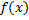 -непрерывна на
-непрерывна на 

Т.Каши:
 -непрерывны на
-непрерывны на  ,дифф. в (a;b) =>
,дифф. в (a;b) => 

Т.Лагранжа является частным случаем т.Каши при g(x)=x
Правило Лопиталя.
Производная помогает раскрыть пределы и раскрывать неопределенности вида:
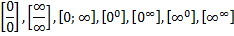
Т.1: 

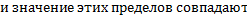
Т.2: 

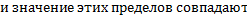
 2018-01-08
2018-01-08 1243
1243
