2018-01-08
860
(остаток в формуле Тейлора в форме Лагранжа) Пусть при всех 
существует 
я производная 
. Тогда для любого 
существует точка 
, лежащая между и 
(то есть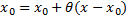 
при 
), такая что
(Остаточный член формулы Тейлора, представленный в таком виде, называется остаточным членом в форме Лагранжа.)
Необходимое и достаточное условие постоянства функции.
Теорема
Пусть функция f (x) определена в промежутке X и имеет внутри него конечную производную f /(x), а на концах (если они принадлежат X) сохраняет непрерывность. Для того чтобы f (x) была в X постоянной, достаточно условие f '(x)=0 внутри X.
Доказательство
Пусть это условие выполнено. Фиксируем некоторую точку x 0 из промежутка X и возьмем любую другую его точку x. Для промежутка [ 
] или [ 
] удовлетворены все условия теоремы Лагранжа. Следовательно, можем написать
f (x)− f (x 0)= f '(c)(x − x 0),
где c содержится между и 
, а значит, заведомо лежит внутри X. Но, по предположению, 
, так что для всех x из X
f (x)= f ()= const.
Теорема доказана.
Достаточное условие монотонности функции.
(Достаточное условие строгой монотонности функции, имеющей производную на интервале)
Пусть функция 
непрерывна на 
и имеет в каждой точке 
производную 
Тогда:
если 
то 
строго возрастает на 
если 
то строго убывает на 
