Первое достаточное условие экстремума:
Пусть функция y = f(x) дифференцируема в 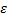 -окрестности точки
-окрестности точки  , а в самой точке
, а в самой точке  непрерывна. Тогда:
непрерывна. Тогда:
- если
 при
при 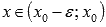 и
и  при
при  , то
, то  - точка максимума;
- точка максимума; - если
 при
при 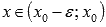 и
и  при
при  , то
, то  - точка минимума.
- точка минимума.
Другими словами:
- если в точке
 функция непрерывна и в ней производная меняет знак с плюса на минус, то
функция непрерывна и в ней производная меняет знак с плюса на минус, то  - точка максимума;
- точка максимума; - если в точке
 функция непрерывна и в ней производная меняет знак с минуса на плюс, то
функция непрерывна и в ней производная меняет знак с минуса на плюс, то  - точка минимума.
- точка минимума.
Второй достаточный признак экстремума функции:
Пусть 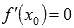 ,
,
- если
 , то
, то  - точка минимума;
- точка минимума; - если
 , то
, то  - точка максимума.
- точка максимума.
Как видно, этот признак требует существования производной как минимум до второго порядка в точке  .
.
Наибольшим значением функции y = f(x) на промежутке X называют такое значение  , что для любого
, что для любого  справедливо неравенство
справедливо неравенство  .
.
Наименьшим значением функции y = f(x) на промежутке X называют такое значение  , что для любого
, что для любого  справедливо неравенство
справедливо неравенство  .
.
 2018-01-08
2018-01-08 723
723








