| sin x = a | sin x = a, а>1 или а<1 | Уравнение корней не имеет | n  Z Z
|
| sin x = -1 | х =  n n
| ||
| sin x = 0 | х =  n n
| ||
| sin x = 1 | х =  n n
| ||
| sin x = a, -1<а<1 | х = 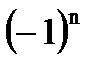 arcsin a + arcsin a +  n n
|
| cos x = a | cos x = a, а>1 или а<1 | Уравнение корней не имеет | n  Z Z
| |
| cos x = -1 | х =  n n
| |||
| cos x = 0 | х =  n n
| |||
| cos x = 1 | х =  n n
| |||
| cos x = a, -1<а<1 | х = 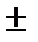 arccos a + arccos a +  n n
| |||
| tgx = a | tg x = 0 | х = 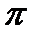 n n
| n  Z Z
| |
| tg x = a | х = arctg a +  n n
| |||
| сtgx = a | ctg x = 0 | х =  n n
| n  Z Z
| |
| ctg x = a | х = arcctg a +  n n
|


ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ

ПРЕОБРАЗОВАНИЕ ГРАФИКОВ ФУНКЦИЙ
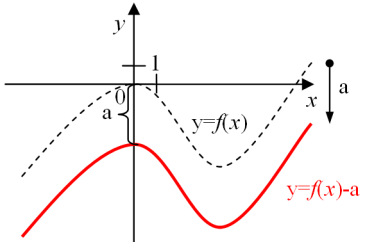
| y = f (x) + a (a >0) | y = f (x) - a (a >0) | |
| Сдвиг графика функции y = f (x) на а единиц | ||
вверх

| вниз
| |
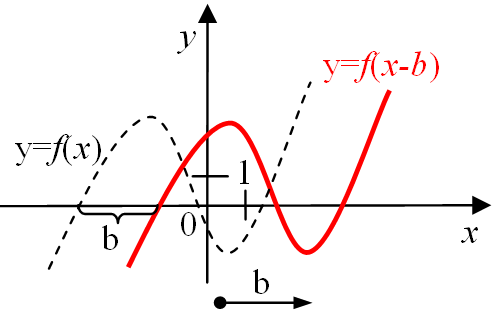
| y = f (x + b) (b >0) | y = f (x - b) (b >0) | |
| Сдвиг графика функции y = f (x) на b единиц | ||
влево

| вправо
| |
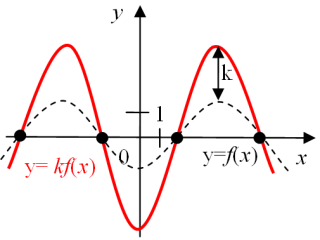
| y = k·f (x) (k >1) | y =  ·f (x) (k >1) ·f (x) (k >1)
| |
| Растяжение | Сжатие | |
| графика функции y=f(x) в k раз вдоль оси OY Точки на оси OX остаются неподвижными. Расстояние от каждой точки до оси OX | ||
| увеличивается в k раз | уменьшается | |
| 
| |
| y = f (kx) (k >1) | y =  (k >1) (k >1)
| |
| Сжатие | Растяжение | |
| графика функции y=f(x) в k раз вдоль оси OX Точки на оси OY остаются неподвижными. Расстояние от каждой точки до оси OY | ||
| уменьшается в k раз | увеличивается | |

| 
| |
y =  f (x) f (x)
| y =| f (x)| | |
| Отражение относительно оси OX | ||
графика функции y = f (x)

| части графика функции y = f (x), лежащей ниже оси OX

|
 2018-01-08
2018-01-08 824
824







