2018-01-08
839
Для того чтобы задать функцию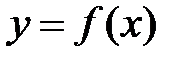 
, необходимо указать определенное правило, по которому для каждого значения 
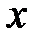можно найти соответствующее значение 
. Различают аналитический, табличный и графическийспособы задания функции.
Аналитический способ:в этом случаефункция задается в виде одной или нескольких формул или уравнений.
Пример 2.1. Примеры аналитически заданных функций:
а)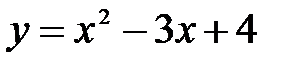 
; б) 
в) 
.
Табличный способ: в этом случае функция задается таблицей ряда значений аргумента и соответствующих значений функции. Например, известные таблицы значений тригонометрических функций, логарифмические таблицы. На практике часто приходится пользоваться таблицами значений функций, полученных в ходе наблюдений или эксперимента.
Графический способ: задается график функции. Преимуществом графического способа является его наглядность, недостатком – его неточность.
Примеры 2.2. Найти область определения функций:
1) 
.
Решение: Функция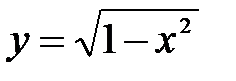 
определена, если подкоренное выражение неотрицательно, т.е. 
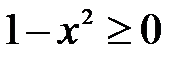. Решая неравенство, получаем, что 
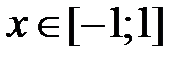, значит, 
.
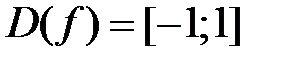2) 
.
Решение: Дробь 
определена, если ее знаменатель не равен нулю. Поэтому область определения данной функции находится из условия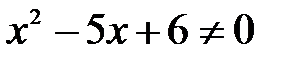 
, т.е. 
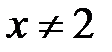и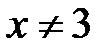 
. Таким образом, 
.
3) 
.
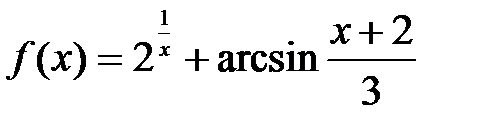Решение: Функция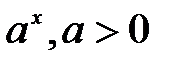 
определена при всех действительных значениях 
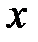, поэтому функция 
определена в точности при тех значениях, при которых имеет смысл выражение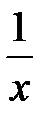 
, т.е. при 
.
Далее, область определения второго слагаемого находим из двойного неравенства 
. Отсюда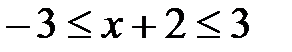 
, т.е. 
.
Область определения функции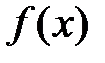 
есть пересечение областей определения обоих слагаемых, откуда 
.
Примеры 2.3. Найти область значений функций:
1) 
.
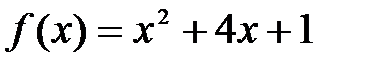Решение: Так как 
, а 
для всех значений 
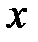, то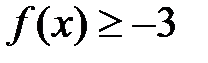 
для всех 
. Поскольку к тому же функция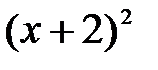 
принимает все значения от 0 до 
, то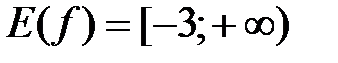 
.
2) 
.
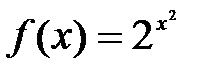Решение: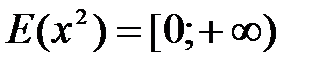 
, поэтому область значений функции 
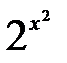совпадает с областью значений функции 
при 
. Тогда 
.
3) 
.
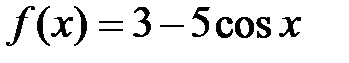Решение: 
, откуда 
. Так как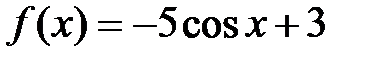 
, то 
.
