2018-01-08
5113
Формула 
также определяет непосредственную функциональную зависимость 
от 
. Однако в некоторых случаях приходится использовать так называемое параметрическое представление функции.
Определение 2.19. Функцией,заданной параметрически, называется функция, у которой каждый аргумент зависит от некоторого параметра. Общий вид функции, заданной параметрически:
где функции 
и 
определены на некотором множестве 
. Переменную 
называют параметром.
Пример 2.14. Примеры функций, заданных параметрически:
а)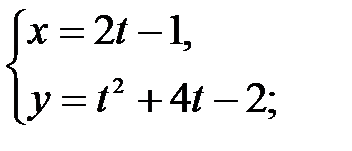 
б) 
в) 
Определение 2.20. Пусть на некотором множестве 
заданы две функции 
и 
. Тогда множество всех точек на плоскости 
с координатами 
, где 
, называется кривой (или линией), заданной параметрически.
