Определение 1.1. Под множеством понимается совокупность объектов, которые объединены по какому-то признаку. Так, можно говорить о множестве студентов в группе, о множестве букв алфавита, о множестве корней квадратного уравнения, о множестве натуральных чисел и т.д. Под элементами множества понимают объекты, из которых состоит это множество. Множества обозначают заглавными буквами латинского алфавита 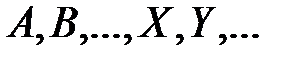 , а их элементы – малыми буквами
, а их элементы – малыми буквами 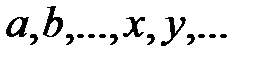
Элемент 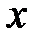 , принадлежащий множеству
, принадлежащий множеству 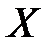 , записывается следующим образом
, записывается следующим образом 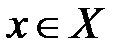 . В противном случае для указания, что элемент
. В противном случае для указания, что элемент 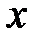 не принадлежит множеству
не принадлежит множеству 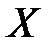 , используется запись
, используется запись 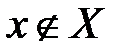 .
.
Определение 1.2. Множество называется пустым, если оно не содержит ни одного элемента. Обозначается символом  .
.
Элементы множества записывают в фигурных скобках, внутри которых они перечислены (если это возможно), либо указано общее свойство, которым обладают все элементы данного множества. Так, запись 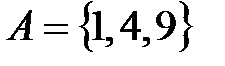 означает, что множество
означает, что множество 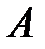 состоит из трех чисел 1, 4 и 9; запись
состоит из трех чисел 1, 4 и 9; запись 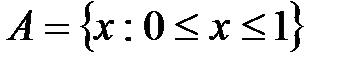 означает, что множество
означает, что множество 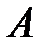 состоит из всех действительных (если не оговорено иное) чисел, удовлетворяющих неравенству
состоит из всех действительных (если не оговорено иное) чисел, удовлетворяющих неравенству 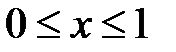 .
.
Множества подразделяются на конечные и бесконечные множества. Множество, число элементов которого конечно, называется конечным. В противном случае множествоназывается бесконечным.
Определение 1.3. Множество 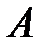 называется подмножеством множества
называется подмножеством множества 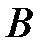 , если каждый элемент множества
, если каждый элемент множества 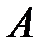 является элементом множества
является элементом множества 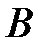 . Символически это обозначают так:
. Символически это обозначают так:  («множество
(«множество 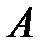 включено во множество
включено во множество 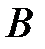 »).
»).
Определение 1.4. Множества 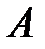 и
и 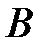 равны, если они состоят из одинаковых элементов. Обозначается
равны, если они состоят из одинаковых элементов. Обозначается 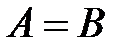 .
.
Над множествами возможны следующие основные операции.
Определение 1.5. Объединением (или суммой) множеств 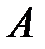 и
и 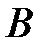 называется множествовсех элементов, принадлежащих хотя бы одному из множеств
называется множествовсех элементов, принадлежащих хотя бы одному из множеств 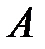 или
или 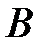 . Обозначается
. Обозначается  .
.
Пример 1.1. Если 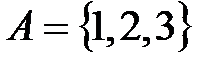 и
и 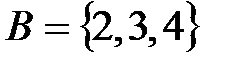 , то
, то 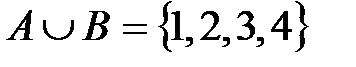 .
.
Определение 1.6. Пересечением (или произведением) множеств 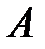 и
и 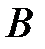 называется множествовсех элементов, принадлежащих каждому из множеств
называется множествовсех элементов, принадлежащих каждому из множеств 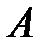 и
и 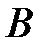 . Обозначается
. Обозначается 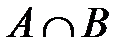 .
.
Пример 1.2. Если 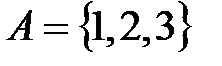 и
и 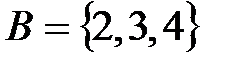 , то
, то 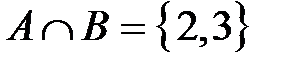 .
.
Определение 1.7. Разностью множеств 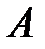 и
и 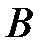 называется множество всех элементов, принадлежащих множеству
называется множество всех элементов, принадлежащих множеству 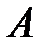 и не принадлежащих множеству
и не принадлежащих множеству 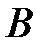 . Обозначается
. Обозначается 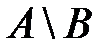 .
.
Пример 1.3. Если 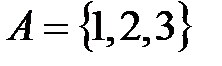 и
и 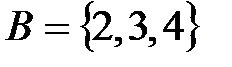 , то
, то 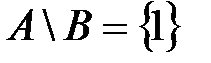 , а
, а 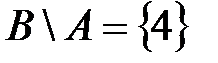 .
.
Числовые множества.
Определение 1.8. Множества, элементами которых являются числа, называются числовыми.
Примерами числовых множеств являются:
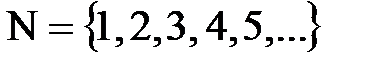 – множество натуральных чисел;
– множество натуральных чисел;
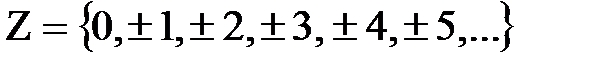 – множество целых чисел;
– множество целых чисел;
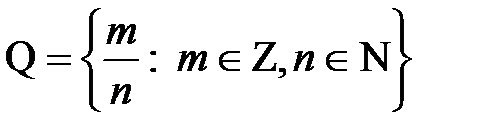 – множество рациональных чисел;
– множество рациональных чисел;
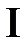 – множество иррациональных чисел;
– множество иррациональных чисел;
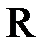 – множество действительных чисел;
– множество действительных чисел;
 – множество комплексных чисел.
– множество комплексных чисел.
Между этими множествами существует соотношение
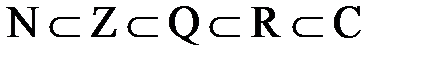 .
.
Множество 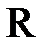 состоит из рациональных и иррациональных чисел. Любое рациональное число может быть выражено либо конечной десятичной дробью
состоит из рациональных и иррациональных чисел. Любое рациональное число может быть выражено либо конечной десятичной дробью 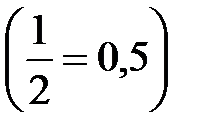 , либо бесконечной периодической дробью
, либо бесконечной периодической дробью 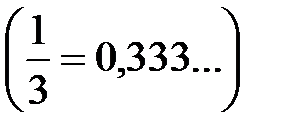 .
.
Действительные числа, которые не являются рациональными, называются иррациональными. Иррациональное число выражается бесконечной непериодической дробью. Так, 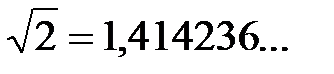 и
и 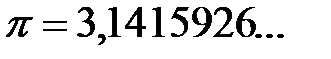 – иррациональные числа.
– иррациональные числа.
Все действительные числа геометрически можно изобразитьточками так называемой числовой прямой (или числовой оси), т.е. прямой, у которой выбраны начало отсчета, положительное направление и единица масштаба.
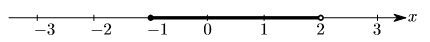
Рис. 1.1. Числовая прямая с отмеченным полуинтервалом 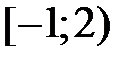 .
.
Между множеством действительных чисел 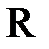 и множеством всех точек числовой прямой существует взаимно-однозначное соответствие, т.е. каждому действительному числу соответствует единственная точка на числовой прямой и, наоборот, каждой точке на числовой прямой соответствует единственное действительное число.
и множеством всех точек числовой прямой существует взаимно-однозначное соответствие, т.е. каждому действительному числу соответствует единственная точка на числовой прямой и, наоборот, каждой точке на числовой прямой соответствует единственное действительное число.
Числовые промежутки.
Различают следующие подмножества множества действительных чисел, определяющие тот или иной числовой промежуток:
1. Если 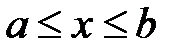 , то говорят, что
, то говорят, что 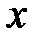 принадлежит отрезку или сегменту
принадлежит отрезку или сегменту 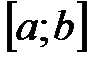 (пишут
(пишут 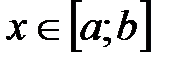 ).
).
2. Если 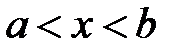 , то
, то 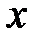 принадлежит интервалу
принадлежит интервалу 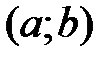 (
(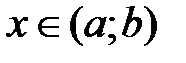 ).
).
3. Если 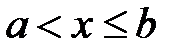 , то
, то 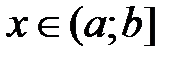 , если
, если 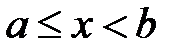 , то
, то 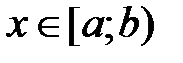 , и говорят, что
, и говорят, что 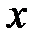 принадлежит полуинтервалу.
принадлежит полуинтервалу.
4. Если 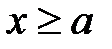 , то
, то 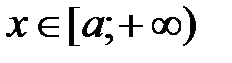 , если
, если 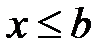 , то
, то 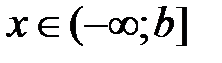 , и говорят, что
, и говорят, что 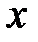 принадлежит бесконечному полуинтервалу.
принадлежит бесконечному полуинтервалу.
5. Если 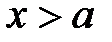 , то
, то 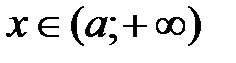 , если
, если 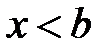 , то
, то 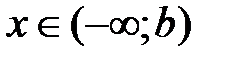 , и говорят, что
, и говорят, что 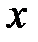 принадлежит бесконечному интервалу.
принадлежит бесконечному интервалу.
6. Если 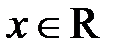 , то
, то 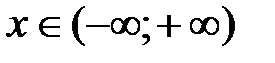 и говорят, что
и говорят, что 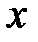 принадлежит множеству действительных чисел или принадлежит всей числовой прямой.
принадлежит множеству действительных чисел или принадлежит всей числовой прямой.
Здесь числа 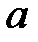 и
и 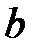 называются соответственно левым и правым концами указанных промежутков. Символы
называются соответственно левым и правым концами указанных промежутков. Символы 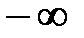 и
и 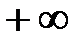 не являются числами, это символическое обозначение процесса неограниченного удаления точек числовой прямой от начала 0 влево и вправо.
не являются числами, это символическое обозначение процесса неограниченного удаления точек числовой прямой от начала 0 влево и вправо.
Определение 1.9. Абсолютной величиной (или модулем)действительного числа 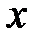 называется само число
называется само число 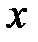 , если
, если 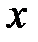 неотрицательно, и противоположное число
неотрицательно, и противоположное число 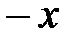 , если
, если 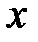 отрицательно:
отрицательно:
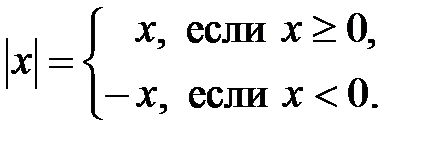
Очевидно, что 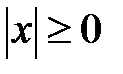 . Запись
. Запись 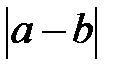 геометрически означает расстояние между точками
геометрически означает расстояние между точками 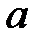 и
и 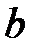 на числовой прямой.
на числовой прямой.
Окрестность точки.
Определение 1.10. Окрестностью точки 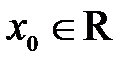 называется любой интервал
называется любой интервал 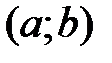 , содержащий точку
, содержащий точку 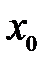 .
.
Определение 1.11. 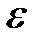 - окрестностью точки
- окрестностью точки 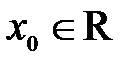 называется интервал
называется интервал 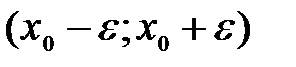 . При этом число
. При этом число 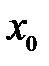 называют центром, а число
называют центром, а число 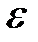 называют радиусом
называют радиусом 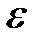 -окрестности.
-окрестности.
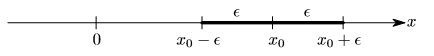
Рис. 1.2. (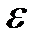 -окрестность).
-окрестность).
Если 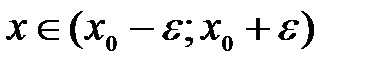 , то выполняется неравенство
, то выполняется неравенство 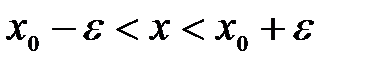 , или, что то же самое,
, или, что то же самое, 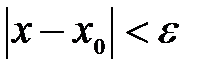 . Последнее неравенство в свою очередь означает, что точка
. Последнее неравенство в свою очередь означает, что точка 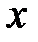 попадает в
попадает в 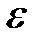 -окрестностьточки
-окрестностьточки  .
.
 2018-01-08
2018-01-08 1446
1446
