2018-01-08
2463
Определение 2.12. Основными элементарными функциями называются следующие функции:
1. Степенная функция – это функция вида 
, где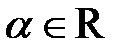 
.
Частные случаи:
– если 
, то получаем так называемые рациональные функции 
;
– если 
(где 
– множество целых отрицательных чисел), то получаем так называемые дробно-рациональные функции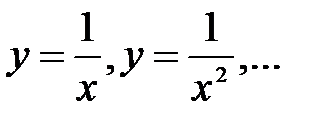 
;
– если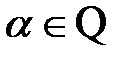 
, т.е. 
,то получаем радикал 
.
Примеры графиков степенных функций, которые соответствуют разным показателямстепени, представлены на рис. 2.2. 
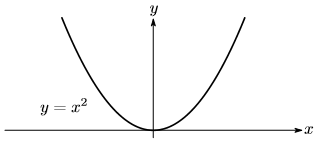
Рис. 2.2.Графики функций 
.
2. Показательная функция – это функция вида 
, где 
. Графики показательных функций представлены на рис. 2.3.
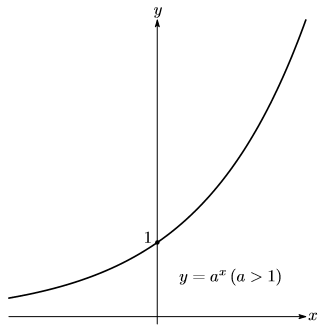
Рис. 2.3.Графики функций 
и 
.
Частный случай: если 
, то получаем так называемую экспоненциальную функцию (или экспоненту) 
, где число 
3. Логарифмическая функция – это функция вида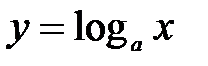 
, где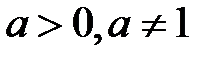 
. Графики логарифмических функций представлены на рис. 2.4.
Рис. 2.4.Графики функци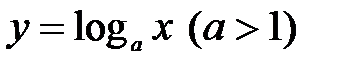й 
и 
.
Частные случаи:
– если , то получаем так называемый натуральный логарифм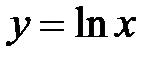 
;
– если 
, то получаем так называемый десятичный логарифм 
.
4. Тригонометрические функции – это функции 
. Графики тригонометрических функций представлены на рис. 2.5.
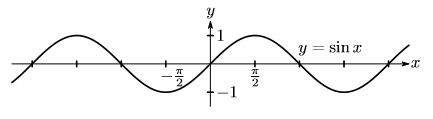
Рис. 2.5.Графики функций 
.
5. Обратные тригонометрические функции – это функции 
. Графики обратных тригонометрических функций представлены на рис. 2.6.
Рис. 2.6.Графики функций 
.
Определение 2.13. Функции, полученные из основных элементарных функций с помощью конечного числа алгебраических операций (сложения, вычитания, умножения, деления) и операции суперпозиции функций, называются элементарными.
Пример 2.10. Примеры элементарных функций:
а) 
; б) 
.
Пример 2.11. Примеры неэлементарных функций:
а) 
б)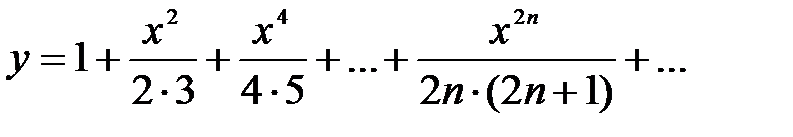 
Определение 2.14. Функция вида
,
где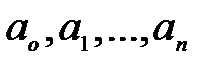 
– постоянные числа, называется многочленом. Число 
называют степенью многочлена.
Определение 2.15. Функция вида
,
где 
– многочлены, называется рациональной функцией.
Определение 2.16. Функции, построенные с помощью суперпозиции рациональных функций и степенных функций с рациональными показателями, называются иррациональными.
Пример 2.12. Примеры иррациональных функций:
а) 
; б) 
.
Неявная функция.
Формула 
определяет явный способ задания функции. Однако во многих случаях приходится использовать неявный способ задания функции.
Определение 2.17. Пусть функция определена на множестве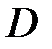 
. Тогда, если каждое значение 
и соответствующее ему значение функции 
удовлетворяют некоторому (одному и тому же) уравнению 
, то говорят, что эта функция задана неявно уравнением 
. Сама функция в этом случае называется неявной функцией.
Пример 2.13. Примеры неявных функций:
а) 
; б) 
; в) 
.
Определение 2.18. Графиком неявной функции, заданной уравнением 
, называется множество всех точек координатной плоскости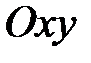 
, координаты которых удовлетворяют этому уравнению.
