2018-01-08
785
«Непрерывность функции».
Задание 1. Пользуясь определением, доказать непрерывность функции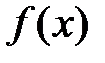 
в каждой точке 
:
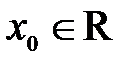1.1.  .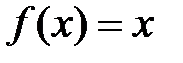
| 1.2.  .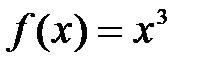
| 1.3.  .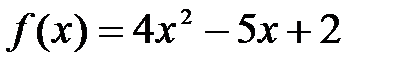
|
Задание 2. Доказать, что функция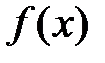 
не является непрерывной в определенной точке 
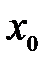. Построить график функции 
.
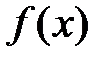2.1.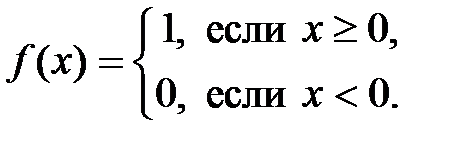 
| 2.2.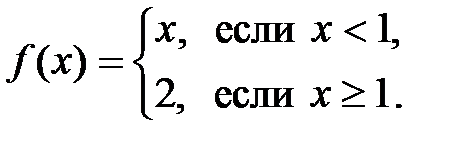 
|
2.3.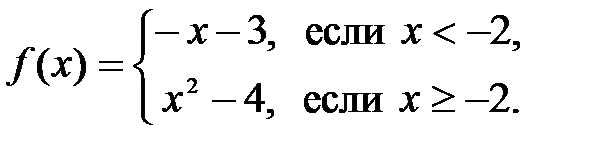 
| 2.4.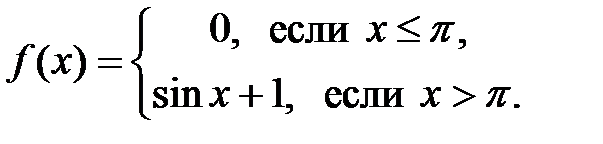 
|
Задание 3. Исследовать на непрерывность и построить график функции 
. Найти скачок функции в точках разрыва.
3.1.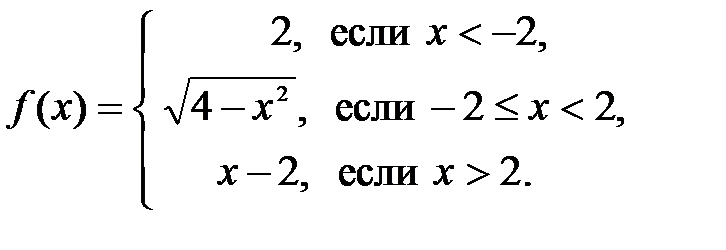 
| 3.2.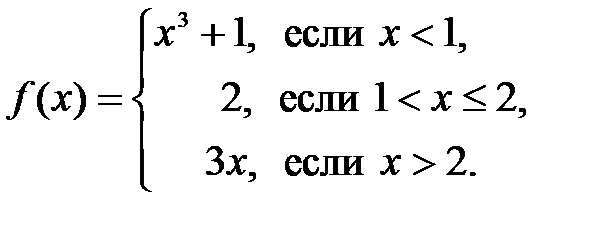 
|
3.3.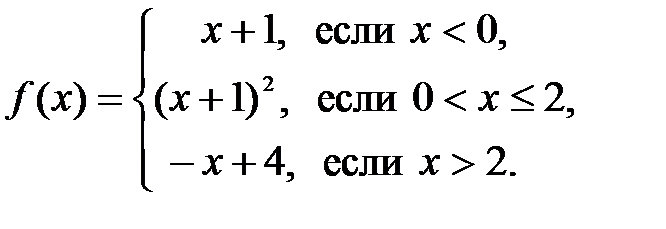 
| 3.4.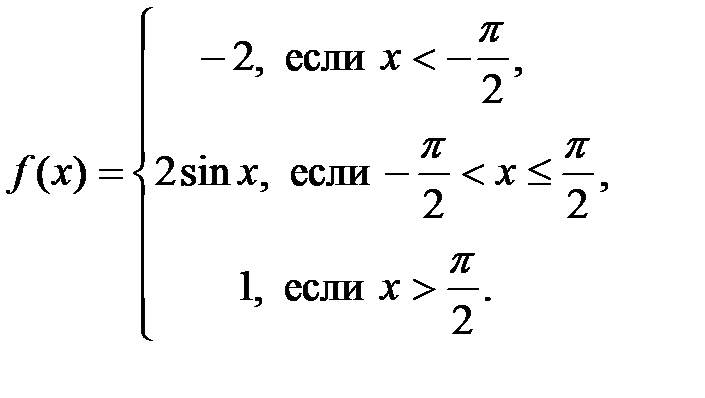 
|
3.5.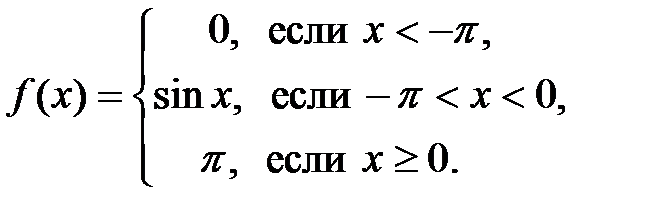 
| 3.6.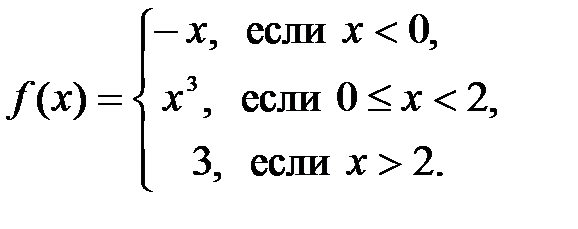 
|
Задание 4. Исследовать на непрерывностьфункцию 
в точке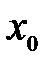 
:
4.1.  .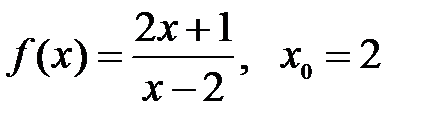
| 4.2.  .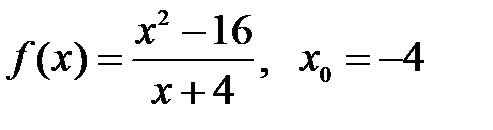
|
4.3.  .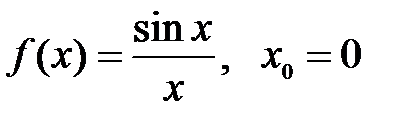
| 4.4.  .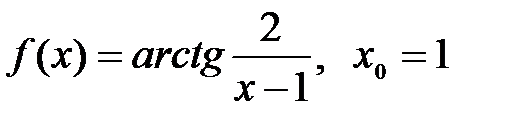
|
4.5.  .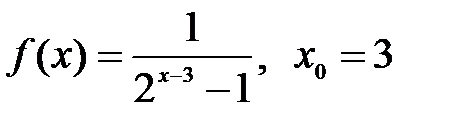
| 4.6.  .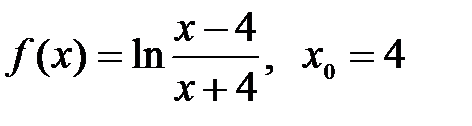
|
Задание 5. Найти все точки разрыва данной функции 
:
5.1.  .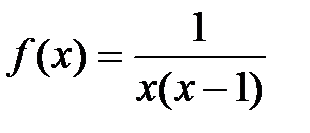
| 5.2.  .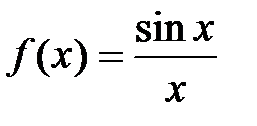
| 5.3.  .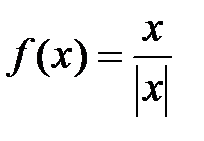
|
5.4.  .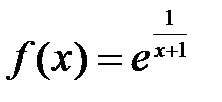
| 5.5.  .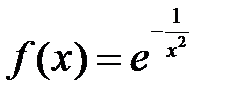
| 5.6.  .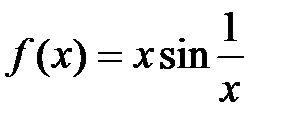
|
Задание 6. Исследовать на непрерывность функцию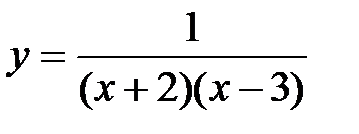 
на отрезке 
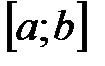, если:
6.1.  .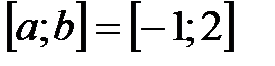
| 6.2.  .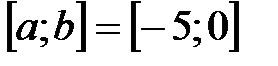
| 6.3.  .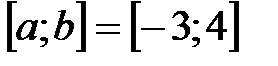
|
Задание 7. Исследовать на непрерывность функцию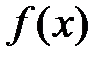 
на отрезках 
, 
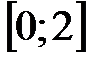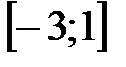и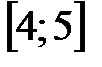 
, если:
7.1.  .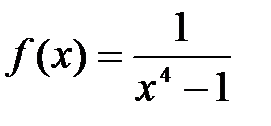
| 7.2.  .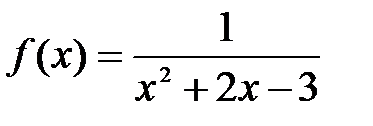
| 7.3.  .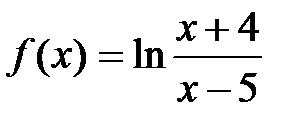
|
Задание 8. При каком значении параметра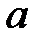 
функция 
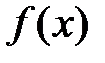будет непрерывной:
8.1.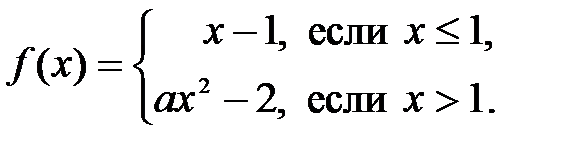 
| 8.2.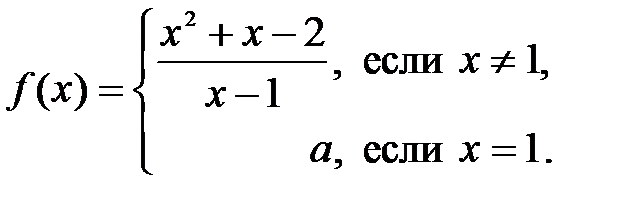 
|
8.3.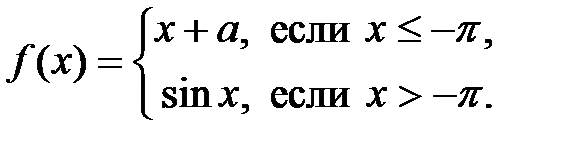 
| 8.4.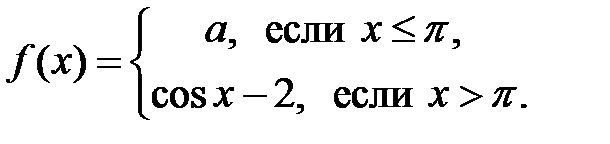 
|
Тема 8. ПРОИЗВОДНАЯ ФУНКЦИИ.
Понятие производной.
Пусть функция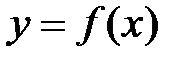 
определена на интервале 
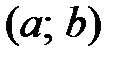. Выберем произвольную точку 
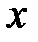из этого интервала и зададим значению 
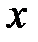приращение 
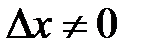. Тогда функция получит соответствующее ему приращение 
.
|
|
|
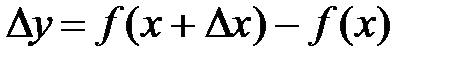Определение 8.1. Производной функции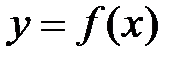 
в точке 
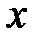называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего к нулю (при условии, что этот предел существует), т.е.
.
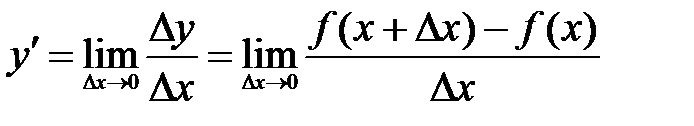Производная функции имеет несколько обозначений: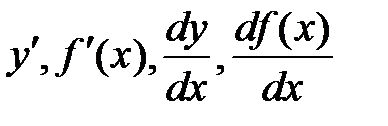 
.
Пример 8.1. Используя определение, доказать, что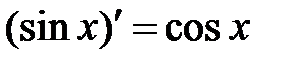 
.
Решение: Найдем приращение функции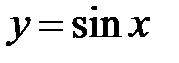 
в точке :
.
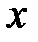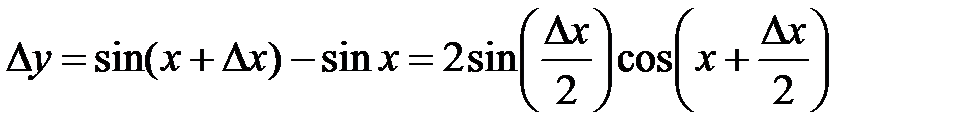Тогда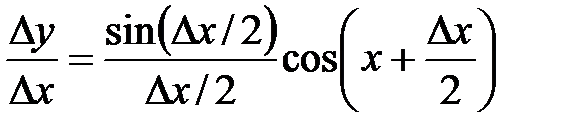 
, где 
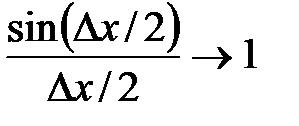при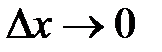 
(попервому замечательному пределу), 
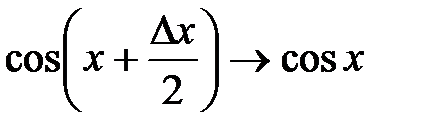(из-за непрерывности функции 
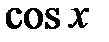). Таким образом, 
.
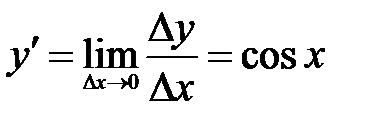Определение 8.2. Операция отыскания производной данной функции называется дифференцированием этой функции.
Определение 8.3. Функция, имеющая в точке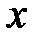 
производную, называется дифференцируемой в этой точке. Функция, дифференцируемая во всех точках интервала 
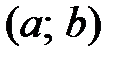, называется дифференцируемой на этом интервале.
