Пусть  есть функция от переменной
есть функция от переменной  (
( ), а переменная
), а переменная  в свою очередь есть функция от независимой переменной
в свою очередь есть функция от независимой переменной  (
( ), т.е. задана сложная функция
), т.е. задана сложная функция 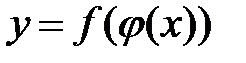 . Функция
. Функция  является внешней функцией, а функция
является внешней функцией, а функция 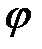 – внутренней.
– внутренней.
Теорема 8.1. Если  и
и  – дифференцируемые функции от своих аргументов, то производная сложной функции
– дифференцируемые функции от своих аргументов, то производная сложной функции 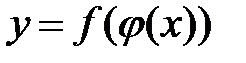 существует и равна произведению производной внешней функции на производную внутренней (или внутренних) функции, т.е.
существует и равна произведению производной внешней функции на производную внутренней (или внутренних) функции, т.е.
 .
.
Пример 8.5. Найти производную функции  .
.
Решение: Исходную функцию можно представить в виде  , где
, где 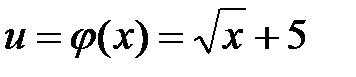 . Тогда, согласно теореме 8.1 о производной сложной функции, будем иметь:
. Тогда, согласно теореме 8.1 о производной сложной функции, будем иметь:
1) 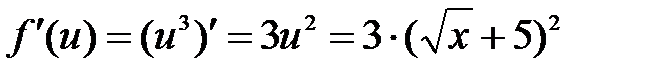 ;
;
2)  ;
;
3)  .
.
Следовательно,  .
.
Логарифмическое дифференцирование.
Определение 8.4. Логарифмическое дифференцирование – это метод отыскания производной заданной функции путем предварительного ее логарифмирования.
Замечание 8.1. Этот метод широко используется для нахождения производной от фукции вида  , где
, где  и
и 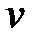 – функции аргумента
– функции аргумента 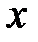 . Действительно, логарифмируя обе части исходного равенства, получаем
. Действительно, логарифмируя обе части исходного равенства, получаем
 .
.
Дифференцируя последнее соотношение, имеем
 .
.
Умножая обе части этого равенства на  и заменяя затем
и заменяя затем  через
через  , после простых преобразований окончательно получаем, что
, после простых преобразований окончательно получаем, что
 .
.
Пример 8.6. Найти производную функции 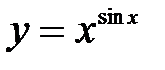 .
.
Решение: Применим метод логарифмического дифференцирования:
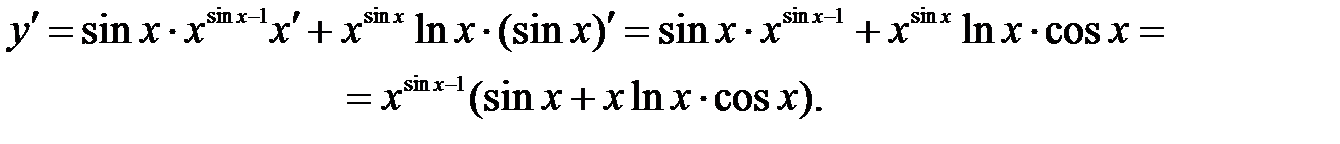
 2018-01-08
2018-01-08 434
434








