Определение 7.8. Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции.
Если 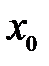 – точка разрыва функции
– точка разрыва функции 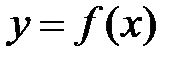 , то в ней не выполняется по крайней мере одно из условий первого определения непрерывности функции, а именно:
, то в ней не выполняется по крайней мере одно из условий первого определения непрерывности функции, а именно:
1. Функция определена в окрестности точки  , но не определена в самой точке
, но не определена в самой точке  .
.
Пример 7.3. Функция 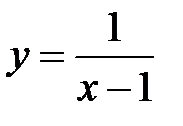 не определена в точке
не определена в точке 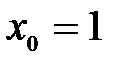 , но определена в ее окрестности. Поэтому
, но определена в ее окрестности. Поэтому 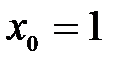 – точка разрыва функции.
– точка разрыва функции.
2. Функция определена в точке 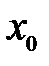 и ее окрестности, но не существует предела
и ее окрестности, но не существует предела 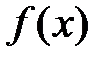 при
при 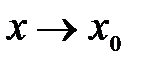 .
.
Пример 7.4. Функция
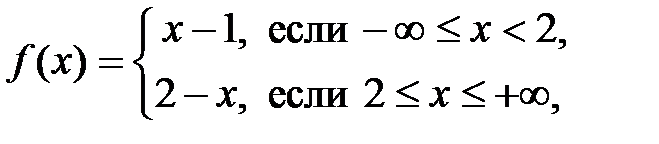
определена в точке  :
:  , но в точке
, но в точке 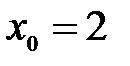 имеет разрыв, т.к. при
имеет разрыв, т.к. при 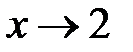 функция предела не имеет: левосторонний и правосторонний пределы различны
функция предела не имеет: левосторонний и правосторонний пределы различны
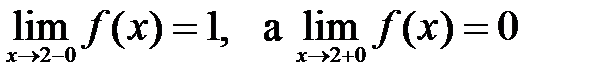 .
.
3. Функция определена в точке  и ее окрестности, существует
и ее окрестности, существует  , но этот предел не равен значению функции в точке
, но этот предел не равен значению функции в точке 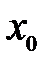 :
:  .
.
Пример 7.5. Функция
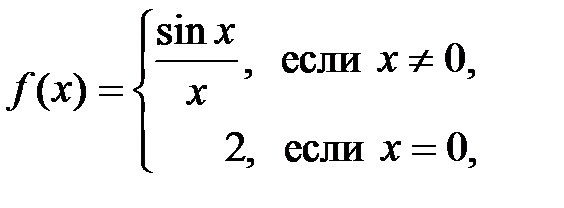
имеет разрыв в точке 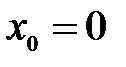 , так как
, так как 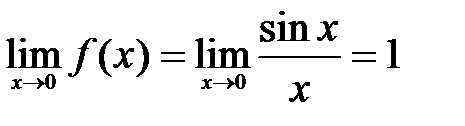 и
и 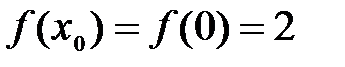 , т.е.
, т.е. 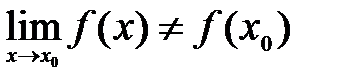 .
.
Все точки разрыва функции подразделяют на точки разрыва первого и второго рода.
Определение 7.9. Точка разрыва 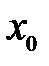 называется точкой разрыва первого рода функции
называется точкой разрыва первого рода функции 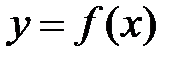 , если в этой точке существуют конечные пределы функции слева и справа (односторонние пределы), т.е.
, если в этой точке существуют конечные пределы функции слева и справа (односторонние пределы), т.е. 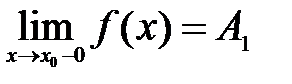 и
и  . При этом:
. При этом:
а) если 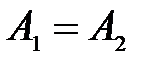 , то точка
, то точка  называется точкой устранимого разрыва;
называется точкой устранимого разрыва;
б) если 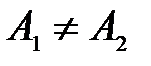 , то точка
, то точка  называется точкой конечного разрыва. Величину
называется точкой конечного разрыва. Величину 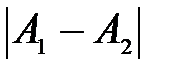 называют скачком функции в точке разрыва первого рода и обозначают
называют скачком функции в точке разрыва первого рода и обозначают  , т.е.
, т.е.
 .
.
Определение 7.10. Точка разрыва 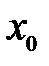 называется точкой разрыва второго рода функции
называется точкой разрыва второго рода функции 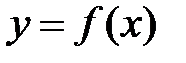 , если по крайней мере один из односторонних пределов
, если по крайней мере один из односторонних пределов  или
или 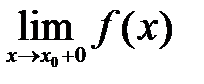 не существует или равен бесконечности.
не существует или равен бесконечности.
Так, для функции 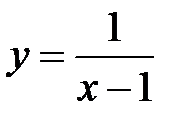 (см. пример 7.3) точка
(см. пример 7.3) точка  является точкой разрыва второго рода.
является точкой разрыва второго рода.
Для функции
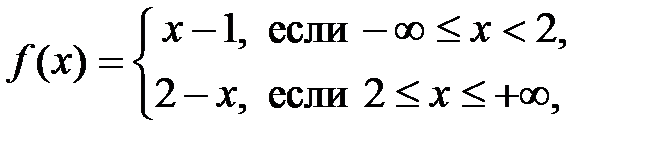
(см. пример 7.4) точка 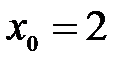 – точка разрыва первого рода (конечный разрыв). Легко определить скачок функции в данной точке разрыва:
– точка разрыва первого рода (конечный разрыв). Легко определить скачок функции в данной точке разрыва:  .
.
Для функции

(см. пример 7.5) точка  – это точка разрыва первого рода (устранимый разрыв).
– это точка разрыва первого рода (устранимый разрыв).
Пример 7.6. Найти точки разрыва функции 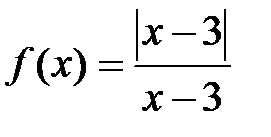 .
.
Решение: Легко видеть, что функция 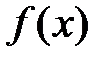 определена и непрерывна в любой точке
определена и непрерывна в любой точке 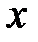 , кроме точки
, кроме точки  . Также очевидно, что
. Также очевидно, что

Значит, 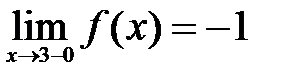 , а
, а 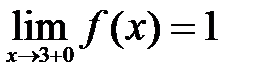 . Поэтому в точке
. Поэтому в точке 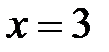 функция терпит разрыв первого рода (конечный разрыв). Скачок функции в этой точке равен
функция терпит разрыв первого рода (конечный разрыв). Скачок функции в этой точке равен  .
.
Пример 5.7. Исследовать на непрерывность функцию
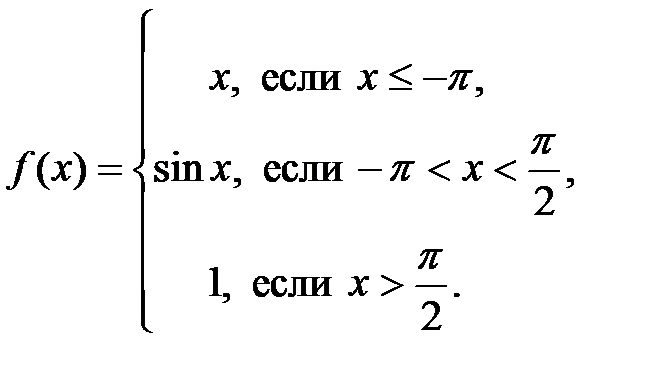
Решение: Функции 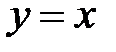 ,
, 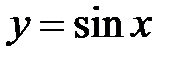 и
и 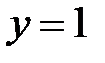 определены и непрерывны в любой точке
определены и непрерывны в любой точке  , поэтому кусочно-заданная функция
, поэтому кусочно-заданная функция  может иметь разрывы только в точках, где изменяется ее аналитическое выражение, т.е. только в точках
может иметь разрывы только в точках, где изменяется ее аналитическое выражение, т.е. только в точках  и
и 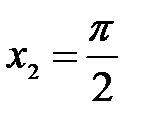 .
.
Исследуем функцию на непрерывность в найденных точках. Для этого найдем односторонние пределы и значение функции в каждой точке в отдельности.
В точке  будем иметь:
будем иметь:
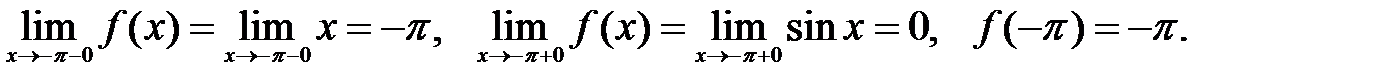
Таким образом,
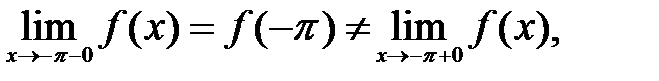
т.е. в точке 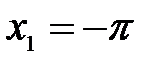 функция имеет разрыв первого рода (конечный разрыв). Скачок функции
функция имеет разрыв первого рода (конечный разрыв). Скачок функции 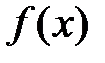 в этой точке равен
в этой точке равен
 .
.
Аналогичным образом для точки 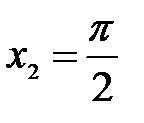 получим:
получим:
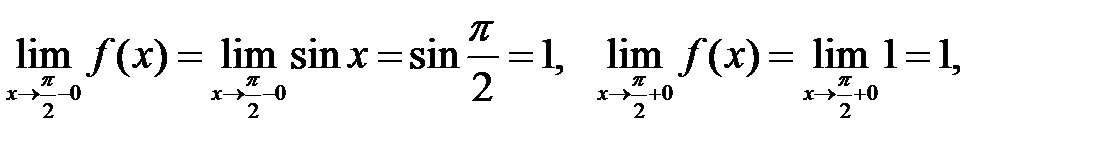
однако значение  не определено. Следовательно,точка
не определено. Следовательно,точка 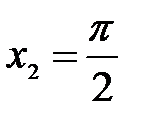 – это точка устранимого разрыва для функции
– это точка устранимого разрыва для функции  .
.
 2018-01-08
2018-01-08 1514
1514
