2018-01-08
993
1.Сумма, разность, произведение и частное двух непрерывных функций есть непрерывная функция (для частного за исключением тех значений аргумента, в которых делитель равен нулю).
2. Если функция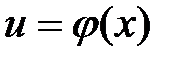 
непрерывна в точке 
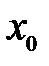, а функция 
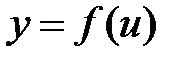непрерывна в точке 
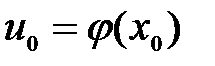, то сложная функция 
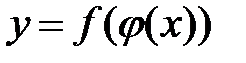также непрерывна в точке 
.
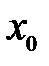3. Если функция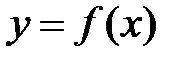 
непрерывна и строго монотонна на 
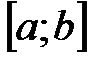оси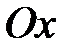 
, то обратная функция 
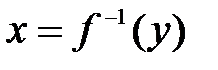также непрерывна и монотонна на соответствующем отрезке 
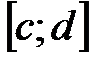оси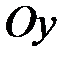 
.
4. Все основные элементарные функции непрерывны в каждой точке своей области определения.
Свойства функций, непрерывных на отрезке.
1. I теорема Больцано-Коши: Если функция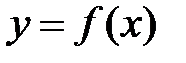 
непрерывна на отрезке 
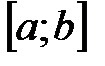и на концах отрезка имеет значения разных знаков, то существует хотя бы одна точка 
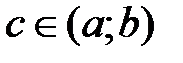, в которой данная функция 
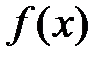обращается в нуль: 
.
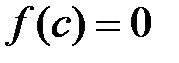2. II теорема Больцано-Коши: Если функция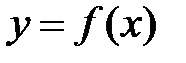 
непрерывна на отрезке 
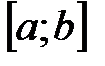и принимает на его концах значения 
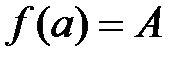и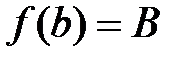 
(
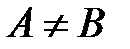), то найдется хотя бы одна внутренняя точка 
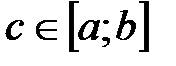, что для любого числа 
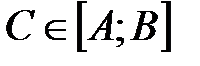выполняется равенство 
.
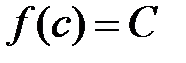3. I теорема Вейерштрасса: Если функция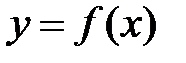 
непрерывна на отрезке 
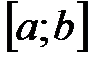, то она ограничена на этом отрезке.
|
|
|
4. II теорема Вейерштрасса: Если функция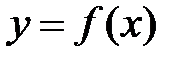 
непрерывна на отрезке 
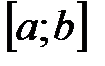, то она достигает на этом отрезке своего наибольшего и наименьшего значений.
