1) Производная суммы (разности) двух дифференцируемых функций равна сумме (разности) производных этих функций:
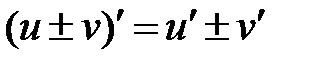 .
.
2) Производная произведения двух дифференцируемых функций равна сумме произведений производной первого сомножителя на второй и производной второго сомножителя на первый:
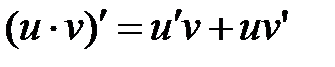 .
.
3) Производная частного двух дифференцируемых функций может быть найдена по формуле:
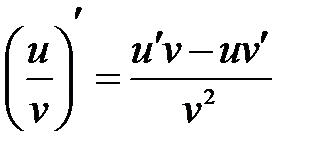 .
.
4) Постоянный множитель можно выносить за знак производной:
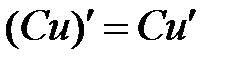 .
.
Таблица производных.
1. 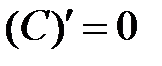 . .
| 2. 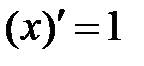 . .
|
3. 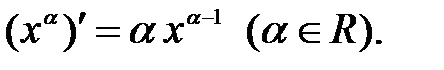
| 4. 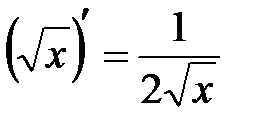 . .
|
5. 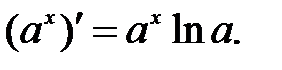
| 6. 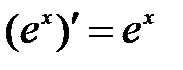
|
7. 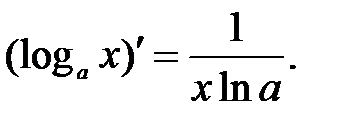
| 8. 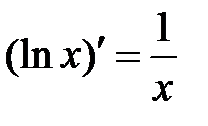 . .
|
9. 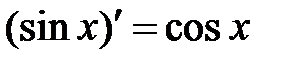 . .
| 10. 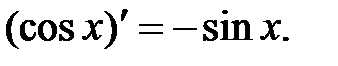
|
11. 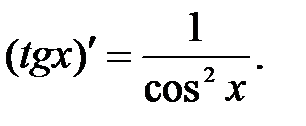
| 12. 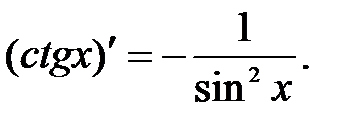
|
13. 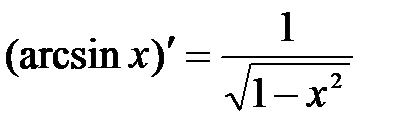 . .
| 14. 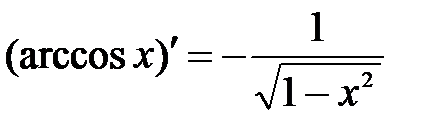 . .
|
15. 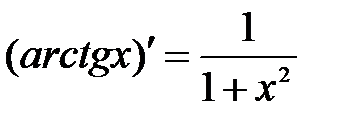 . .
| 16. 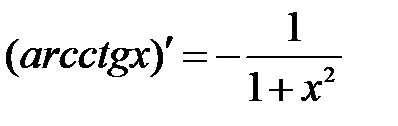 . .
|
Пример 8.2. Найти производную функции 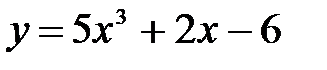 .
.
Решение: Используя правила дифференцирования (1 и 4) и таблицу производных, находим, что
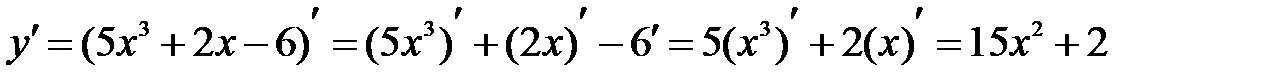 .
.
Пример 8.3. Найти производную функции 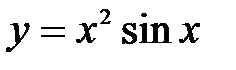 .
.
Решение: Используя правило дифференцирования (2) и таблицу производных, находим, что
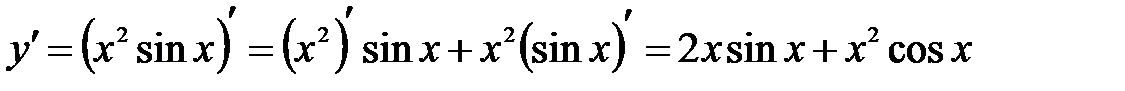 .
.
Пример 8.4. Найти производную функции 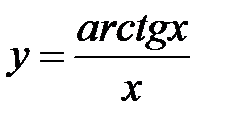 .
.
Решение: Используя правило дифференцирования (3) и таблицу производных, находим, что
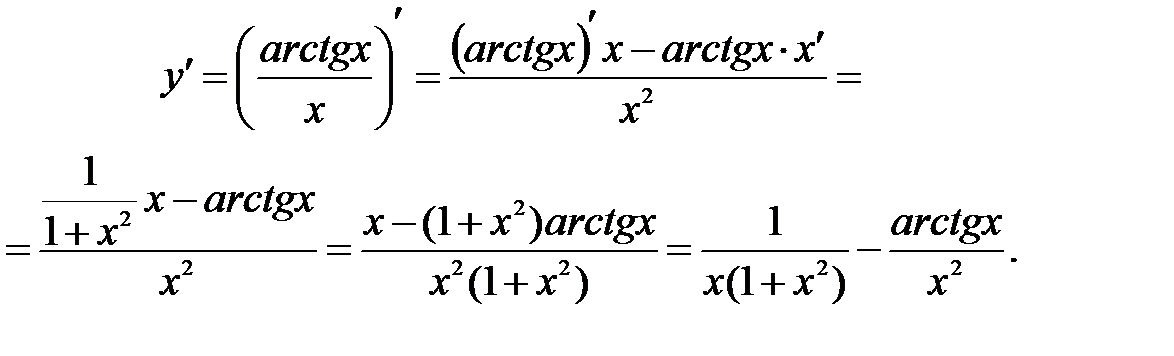
 2018-01-08
2018-01-08 640
640








