Производная неявной функции

Определение 8.5. Если как функция от задается посредством соотношения

,

где – выражение, содержащее и , то 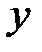называется неявной функциейот .

Для нахождения производной функции , заданной неявно, нужно продифференцировать обе части уравнения, рассматривая как функцию от , а затем из полученного уравнения найти производную .

Пример 8.7. Найти производную функции , которая задана уравнением .

Решение: Дифференцируем обе части равенства, рассматривая как функцию от :

.

Решаем полученное уравнение относительно :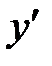

; ; .

Производная функции, заданной параметрически.

Определение 8.6. Переменная ,как функция аргумента , задана параметрически, если обе переменные и заданы как функции некоторой третьей переменной (параметр), т.е.

Предполагаем, что обе функции и дифференцируемы по параметру в рассматриваемом промежутке изменения этого параметра.

Для нахождения производной функции , заданной параметрически, используют формулу:

.

Пример 8.8. Найти производную функции, заданной параметрически .

Решение: Дифференцируем каждую функцию и по переменной :

, ,

откуда

.