«Производная функции».
Задание 1. Используя определение производной, доказать справедливость следующих формул:
1.1.  . .
| 1.2. 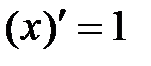 . .
| 1.3.   . .
|
1.4.  . .
| 1.5.  . .
| 1.6.  . .
|
1.7.  . .
| 1.8.  . .
| 1.9.  . .
|
1.10.  . .
| 1.11.  . .
| 1.12.  . .
|
1.13.  . .
| 1.14.  . .
| 1.15. 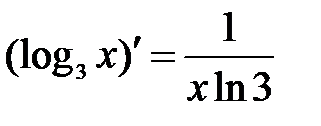 . .
|
Задание 2. Найти производные следующих простых функций:
2.1. 
| 2.2.  . .
| 2.3.  . .
|
2.4.  . .
| 2.5.  . .
| 2.6. 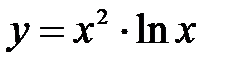 . .
|
2.7.  . .
| 2.8.  . .
| 2.9. 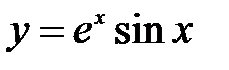 . .
|
2.10.  . .
| 2.11. 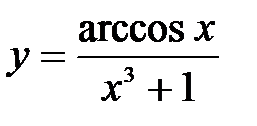 . .
| 2.12.  . .
|
2.13.  . .
| 2.14.  . .
| 2.15.  . .
|
2.16.  . .
| 2.17.  . .
| 2.18.  . .
|
Задание 3. Найти производные следующих сложных функций:
3.1.  . .
| 3.2. 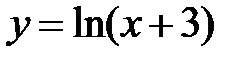 . .
| 3.3.  . .
|
3.4. 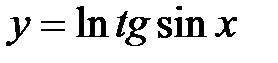 . .
| 3.5. 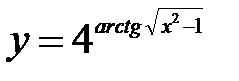 . .
| 3.6. 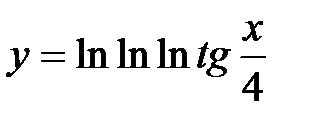 . .
|
3.7. 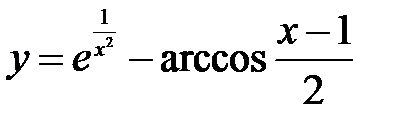 . .
| 3.8.  . .
| 3.9.  . .
|
3.10. 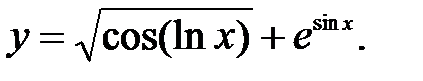
| 3.11.  . .
| 3.12.  . .
|
3.13.  . .
| 3.14. 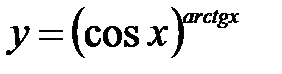 . .
| 3.15.  . .
|
3.16.  . .
| 3.17.  . .
| 3.18. 
|
Задание 4. Найти производные функций, заданных неявно и параметрически:
4.1.  . .
| 4.2.  . .
| 4.3.  . .
|
4.4.  . .
| 4.5.  . .
| 4.6.  . .
|
4.7.  . .
| 4.8.  . .
| 4.9.  . .
|
4.10. 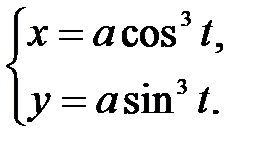
| 4.11. 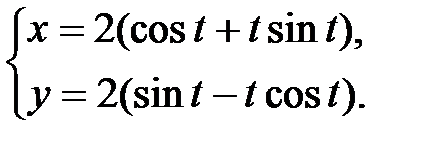
| 4.12. 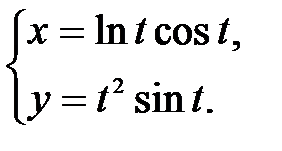
|
4.13. 
| 4.14. 
| 4.15. 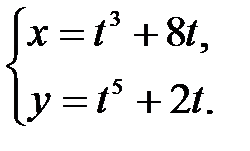
|
4.16. 
| 4.17. 
| 4.18. 
|
Задание 5. Найти значение производной функции в данной точке:
5.1  в точке в точке  . .
| 5.2.  в точке в точке  . .
|
5.3.  в точке в точке  . .
| 5.4.  в точке в точке  . .
|
5.5.  в точке в точке  . .
| 5.6.  в точке в точке  . .
|
Задание 6. Найти уравнение касательной к кривой в точке M:
6.1.  , ,  . .
| 6.2. 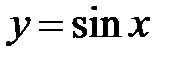 , ,  . .
|
6.3.  , ,  . .
| 6.4.  , ,  . .
|
6.5.  M при M при  . .
| 6.6. 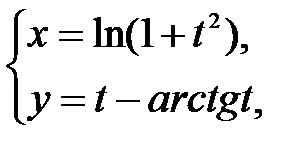 M при M при  . .
|
Задание 7. Найти уравнение нормали к кривой в точке M:
7.1.  , ,  . .
| 7.2.  , ,  . .
|
7.3. 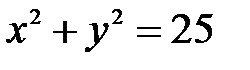 , ,  . .
| 7.4.  , ,  . .
|
7.5.  , M при , M при  . .
| 7.6. 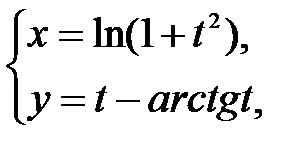 M при M при  . .
|
Задание 8. Определить угол, под которым кривая пересекает ось абсцисс:
8.1.  . .
| 8.2.  . .
| 8.3.  . .
|
8.4.  . .
| 8.5.  . .
| 8.6. 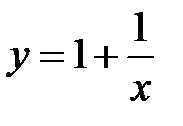 . .
|
Задание 9. Точка движется попрямой, причем расстояние  точки от начала отсчёта, измеряемое в метрах, определяется по формуле
точки от начала отсчёта, измеряемое в метрах, определяется по формуле  , где
, где  – время, измеряемое в секундах. Определить скорость движения точки в конце третьей секунды.
– время, измеряемое в секундах. Определить скорость движения точки в конце третьей секунды.
Задание 10. Путь, проходимый телом, свободно падающим в пустоте, определяется по формуле  . При этом предполагается, что в начальный момент времени тело находится в начале отсчета и начальная скорость равна нулю; g – ускорение свободного падения. Вывести закон изменения скорости свободно падающего тела.
. При этом предполагается, что в начальный момент времени тело находится в начале отсчета и начальная скорость равна нулю; g – ускорение свободного падения. Вывести закон изменения скорости свободно падающего тела.
Задание 11. Радиус шара возрастает равномерно со скоростю 10 см/с. С какой скоростью растет объем шара в момент, когда радиус его составит 100 см?
Задание 12. На кривой  найти точку, в которой ордината возрастает в четыре раза быстрее, чем абсцисса.
найти точку, в которой ордината возрастает в четыре раза быстрее, чем абсцисса.
Задание 13. При каком значении x ордината кривой  будет возрастать в четыре раза быстрее, чем ордината кривой
будет возрастать в четыре раза быстрее, чем ордината кривой  ?
?
 2018-01-08
2018-01-08 674
674








