2018-01-08
655
Геометрический смысл производной. Угловой коэффициент касательной к кривой 
в точке с абсциссой 
равен производной функции 
в этой точке, т.е.
.
Уравнение касательной к кривой 
в точке касания 
имеет вид:
.
Определение 8.7. Прямая, проходящая через точку касания перпендикулярно касательной, называется нормалью к кривой в данной точке.
Уравнение нормали к кривой 
в точке касания 
имеет вид:
.
Пример 8.9. Найти уравнение касательной и нормали к кривой 
в точке 
.
Решение: Для того чтобы найти угловой коэффициент касательной, необходимо вычислить производную от заданной функции:
Значение производной в заданной точке M и определяет искомый угловой коэффициент:
Уравнение касательной: 
или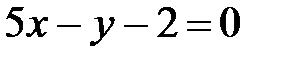 
.
Уравнение нормали: 
или 
.
Физический смысл производной. Значение производной от функции в данной точке характеризует скорость изменения функции в этой точке по сравнению со скоростью возрастания независимого переменного, в частности, скорость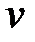 
прямолинейного движения есть производная от пути по времени 
, т.е.
|
|
|
,
а ускорение 
есть производная от скорости, т.е.
,
или вторая производная от пути, т.е.
.
Пример 8.10. Точка движется попрямой, причем расстояние 
точки от начала отсчета, измеряемое в метрах, определяется по формуле 
, где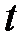 
– время, измеряемое в секундах. Определить скорость движения точки в конце пятой секунды.
Решение: Используя физический смысл производной, находим, что скорость движения в любой момент времени определяется формулой 
а скорость движения в конце пятой секунды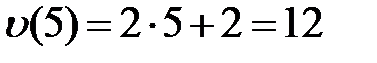 
(м/с).
