2018-01-08
597
«Производные и дифференциалы высших порядков».
Задание 1. Найти производные и дифференциалы указанного порядка:
1.1.  , второй порядок.
| 1.2.  , второй порядок.
|
1.3.  , второй порядок.
| 1.4.  , третий порядок.
|
1.5.  , четвертый порядок.
| 1.6.  , третий порядок.
|
Задание 2. Найти производные и дифференциалы 
-го порядка:
2.1.  .
| 2.2.  .
| 2.3.  .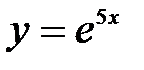
|
2.4.  .
| 2.5.  .
| 2.6.  .
|
Задание 3. Найти производные и дифференциалы второго порядка:
3.1.  .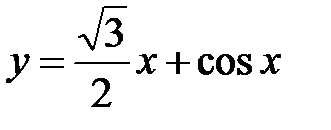
| 3.2.  .
| 3.3.  .
|
3.4.  .
| 3.5.  .
| 3.6. .
|
3.7.  .
| 3.8.  .
| 3.9.  .
|
3.10.  .
| 3.11.  .
| 3.12.  .
|
3.13.  .
| 3.14.  .
| 3.15.  .
|
3.16. 
| 3.17. 
| 3.18. 
|
Задание 4. Точка движется попрямой, причем расстояние 
точки от начала отсчета, измеряемое в метрах, определяется по формуле 
, где 
– время, измеряемое в секундах. Определить ускорение движения точки в конце второй секунды.
Задание 5. Точка массы 
совершает гармоническое колебание около положения равновесия О по закону 
, где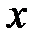 
– расстояние точки от О в момент времени t; 
– постоянные. Показать, что действующая сила пропорциональна расстоянию точки от О.
Тема 11. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ.
Применение дифференциала к приближенным вычислениям.
Определение 11.1. Дифференциал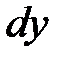 
функции 
и ее приращение 
связаны соотношением
где 
при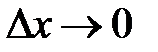 
.
Поэтому при малых 
(
) имеет место следующее приближенное равенство:
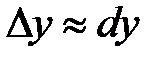
или
Это соотношение часто используется в приближенных вычислениях.
Пример 11.1. Найти приближенное значение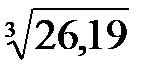 
.
Решение: В данном случае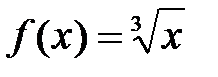 
, 
.
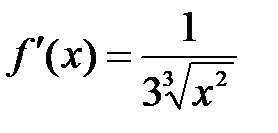1) 
2) 
