Определение 12.1. Функция 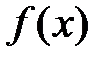 называется монотонно возрастающей на интервале
называется монотонно возрастающей на интервале 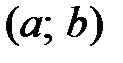 , если для любых
, если для любых 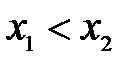 из этого интервала выполнено условие
из этого интервала выполнено условие
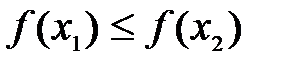 при
при 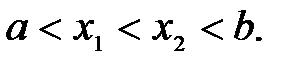
Определение 12.2. Функция 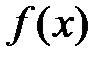 называется монотонно убывающей на интервале
называется монотонно убывающей на интервале 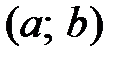 , если для любых
, если для любых 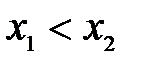 из этого интервала выполнено условие
из этого интервала выполнено условие
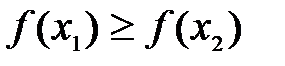 при
при 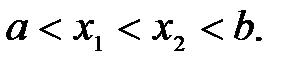
Перечисленные выше условия называются условиями монотонности в широком смысле. Если в них знак равенства исключен, то функция  называется строго монотонной.
называется строго монотонной.
Теорема 12.1. Дифференцируемая функция  является монотонно возрастающей на интервале
является монотонно возрастающей на интервале 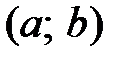 тогда и только тогда, когда
тогда и только тогда, когда
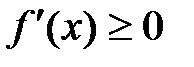 при
при 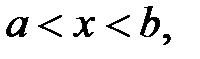
и является монотонно убывающей, если
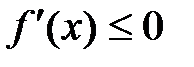 при
при 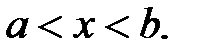
Пример 12.1. Найти интервалы монотонности функции 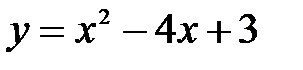 .
.
Решение: Вычисляем производную: 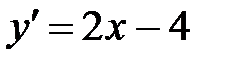 . Очевидно,
. Очевидно, 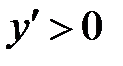 при
при 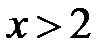 и
и 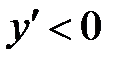 при
при 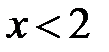 , т.е. функция убывает на интервале
, т.е. функция убывает на интервале 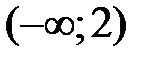 и возрастает на интервале
и возрастает на интервале 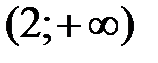 .
.
Экстремумы функции.
Определение 12.3. Точка 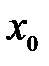 называется точкой максимума функции
называется точкой максимума функции 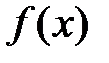 , если в некоторой окрестности этой точкивыполняется неравенство
, если в некоторой окрестности этой точкивыполняется неравенство 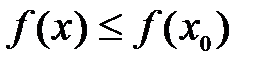 .
.
Определение 12.4. Точка 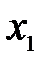 называется точкой минимума функции
называется точкой минимума функции 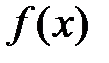 , если в некоторой окрестности этой точки выполняется неравенство
, если в некоторой окрестности этой точки выполняется неравенство 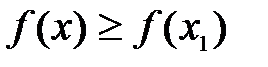 .
.
Значения функции 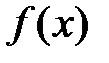 в точках
в точках 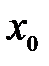 и
и 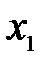 называются соответственно максимумом и минимумом этой функции, объединяемые общим названием экстремумы функции.
называются соответственно максимумом и минимумом этой функции, объединяемые общим названием экстремумы функции.
Необходимое условие существования экстремума. Для того чтобы функция 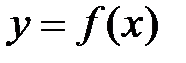 имела экстремум в точке
имела экстремум в точке 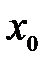 , необходимо, чтобы ее производная в этой точке равнялась нулю (
, необходимо, чтобы ее производная в этой точке равнялась нулю (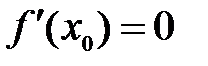 ) или не существовала.
) или не существовала.
Определение 12.5. Точки, в которых выполнено необходимое условие экстремума и которые входят в область определения функции, называются критическими.
Достаточное условие экстремума. Если при переходе через точку 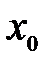 производная дифференцируемой функции
производная дифференцируемой функции 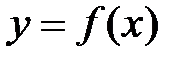 меняет свой знак с «плюса» на «минус», то точка
меняет свой знак с «плюса» на «минус», то точка 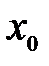 есть точка максимума функции
есть точка максимума функции 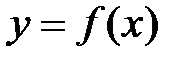 , а если с «минуса»на «плюс»– то точка минимума. Если изменения знака производной не происходит, то экстремума нет.
, а если с «минуса»на «плюс»– то точка минимума. Если изменения знака производной не происходит, то экстремума нет.
Схема исследования функции 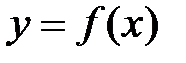 на экстремум:
на экстремум:
1. Найти производную 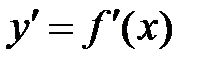 .
.
2. Найти критические точки функции, в которых производная 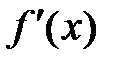 =0 или не существует.
=0 или не существует.
3. Исследовать изменение знака производной при переходе через критическую точку. Сделать вывод о наличии экстремума.
4. Найти экстремумы функции (значения функции в точках экстремума).
Пример 12.2. Определить точки экстремума функции 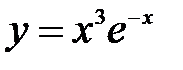 .
.
Решение:
1. Найдем производную заданной функции:
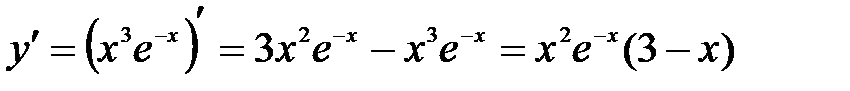 .
.
2. Найдем точки, в которых
производная равна нулю – 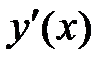 =0:
=0:  при
при 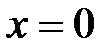 и
и 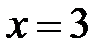 ;
;
производная не существует – таких точек нет.
Значит, критическими являются точки 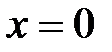 и
и 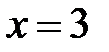 .
.
3. Исследуем изменение знака производной при переходе через критическиеточки:
при 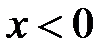
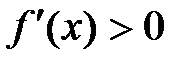 , при
, при 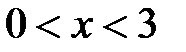
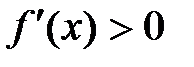 ,при
,при 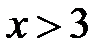
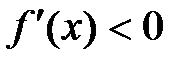 .
.
Таким образом, 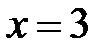 – точка максимума, а
– точка максимума, а 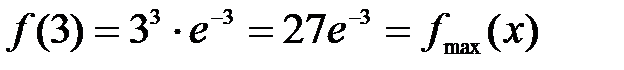 – максимум функции.
– максимум функции.
 2018-01-08
2018-01-08 525
525








