1. Теорема Ролля. Если функция  :
:
1)непрерывна на отрезке  ,
,
2)дифференцируема на интервале  ,
,
3)  ,
,
то найдется по крайней мере одна точка  на интервале
на интервале  , в которой
, в которой 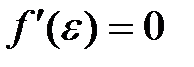 .
.
2. Теорема Лагранжа. Если функция  :
:
1. непрерывна на отрезке  ,
,
2. дифференцируема на интервале  ,
,
то на интервале  найдется по крайней мере одна точка
найдется по крайней мере одна точка  , в которой
, в которой
 .
.
3. Теорема Коши. Если две функции  и
и 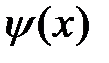 :
:
1. непрерывны на отрезке  ,
,
2. дифференцируемы на интервале  ,
,
3.  на интервале
на интервале  ,
,
то на интервале  найдется по крайней мере одна точка
найдется по крайней мере одна точка  , в которой
, в которой
 .
.
Замечание 11.1. Формулу из теоремы Лагранжа иногда, обозначая  , записывают в следующем виде:
, записывают в следующем виде:
 .
.
Формула Тейлора.
Естественным обобщением последней формулы для функций, имеющих n производных в некоторой окрестности точки  (включая саму эту точку), является формула Тейлора:
(включая саму эту точку), является формула Тейлора:

где  – остаточный член формулы Тейлора, в форме Лагранжа имеющий вид:
– остаточный член формулы Тейлора, в форме Лагранжа имеющий вид:
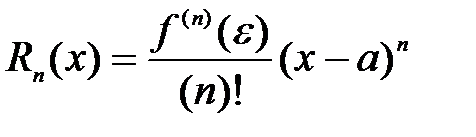
( – некоторая промежуточная точка между точками
– некоторая промежуточная точка между точками  и
и 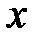 ).
).
Пример 11.2. Проверить справедливость теоремы Лагранжа для функции 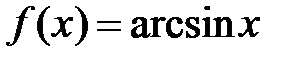 на отрезке
на отрезке  .
.
Решение: Функция  определена и непрерывна на отрезке
определена и непрерывна на отрезке 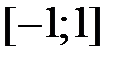 как элементарная функция. Найдем ее производную:
как элементарная функция. Найдем ее производную:  , т.е. функция дифференцируема на интервале
, т.е. функция дифференцируема на интервале  . Следовательно, теорема Лагранжа справедлива для функции
. Следовательно, теорема Лагранжа справедлива для функции  на отрезке
на отрезке 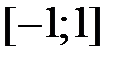 . Поэтому на интервале
. Поэтому на интервале  найдется по крайней мере одна точка
найдется по крайней мере одна точка  , в которой
, в которой
 .
.
Решая данное уравнение относительно  , получим
, получим  .
.
Правило Лопиталя.
Простым приемом для раскрытия неопределенностей вида  и
и  при отыскании предела функций является правило Лопиталя (Гильом Лопиталь (1661-1704) – французский математик).
при отыскании предела функций является правило Лопиталя (Гильом Лопиталь (1661-1704) – французский математик).
Теорема 11.1. Предел отношения двух бесконечно малых или бесконечно больших функций  и
и  равен пределу отношения их производных, если последний существует, т.е.
равен пределу отношения их производных, если последний существует, т.е.
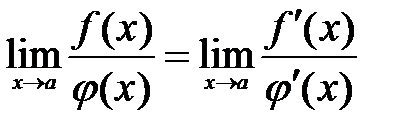 .
.
Пример 11.3. Вычислить  .
.
Решение: Подстановка предельного значения  приводит к неопределенности вида
приводит к неопределенности вида  . Предел отношения производных существует. Тогда
. Предел отношения производных существует. Тогда
 .
.
Замечание 11.2. Если  и
и  при
при  , то отыскание предела
, то отыскание предела  (неопределенность вида
(неопределенность вида  ) может быть сведено к одному из ранее рассмотренных случаев
) может быть сведено к одному из ранее рассмотренных случаев  или
или  путем тождественных преобразований:
путем тождественных преобразований:
 или
или  .
.
Пример 11.4. Вычислить  .
.
Решение: Подстановка предельного значения приводит к неопределенности вида  . Преобразуем функцию так, чтобы получилась неопределенность вида
. Преобразуем функцию так, чтобы получилась неопределенность вида  :
:  . Предел отношения производных существует. Тогда
. Предел отношения производных существует. Тогда
 .
.
Замечание 11.3. Если  и
и 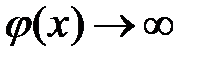 при
при  , тоотыскание предела
, тоотыскание предела  (неопределенность вида
(неопределенность вида  ) может быть сведено к раскрытию неопределенности вида
) может быть сведено к раскрытию неопределенности вида  путем тождественных преобразований:
путем тождественных преобразований:
 или
или  .
.
Пример 11.5. Вычислить  .
.
Решение: Подстановка предельного значения приводит к неопределенности вида  . Преобразуем функцию так, чтобы получилась неопределенность вида
. Преобразуем функцию так, чтобы получилась неопределенность вида 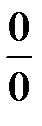 :
:  . Предел отношения производных существует. Тогда
. Предел отношения производных существует. Тогда

Замечание 11.4. При отыскании предела функции вида  могут возникнуть неопределенности вида
могут возникнуть неопределенности вида  . В этих случаях можно прийти к неопределенности вида
. В этих случаях можно прийти к неопределенности вида  путем следующих преобразований:
путем следующих преобразований:
 ,
,
а в силу непрерывности показательной функции:

Пример 11.6. Вычислить  .
.
Решение: Подстановка предельного значения приводит к неопределенности вида 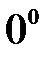 . Преобразуем исходный предел:
. Преобразуем исходный предел:  , где
, где

Тогда 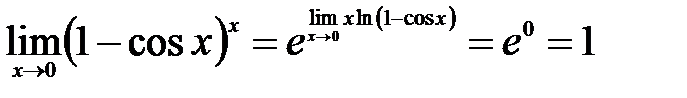 .
.
 2018-01-08
2018-01-08 1227
1227








