2018-01-08
644
1. Интегралы вида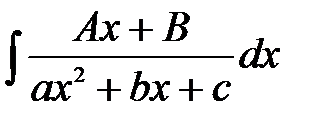 
.
Основной прием вычисления таких интегралов − выделение полного квадрата из квадратного трехчлена, стоящего в знаменателе, и разложение полученного интеграла на сумму двух интегралов.
2. Интегралы вида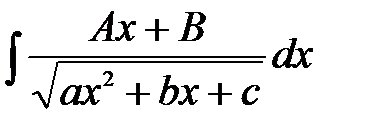 
.
Прием вычисления таких интегралов тот же – следует выделить полный квадрат из квадратного трехчлена подкоренного выражения и разложить на сумму двух интегралов.
Примеры 16. Вычислить интегралы:
1) 
.
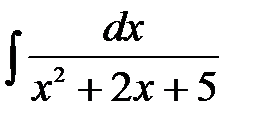Решение: Выделим из квадратного трехчлена полный квадрат:
.
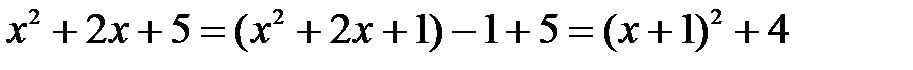Отсюда находим
.
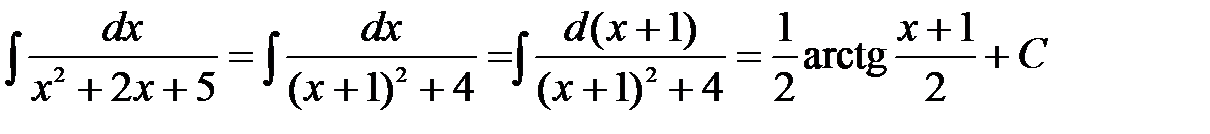2) 
.
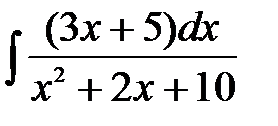Решение: Выделяем полный квадрат из квадратного трехчлена, получаем
.
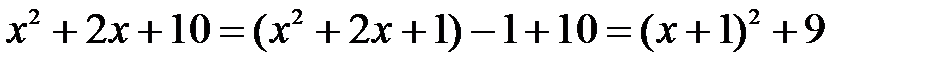Следовательно,
.
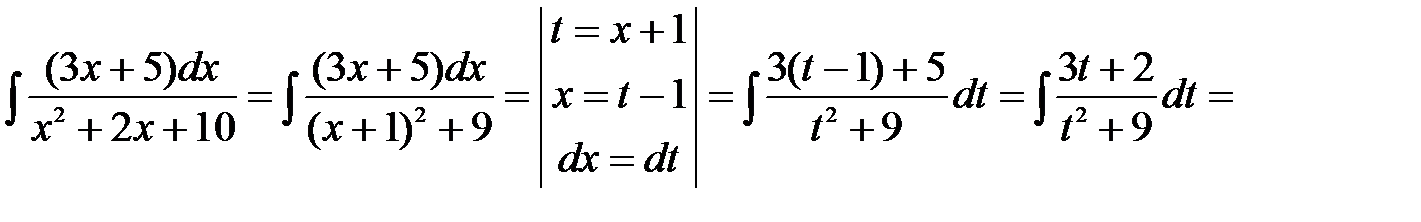
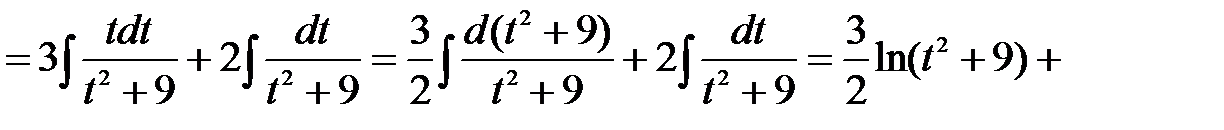
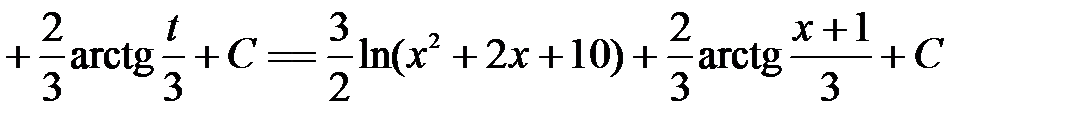3) 
.
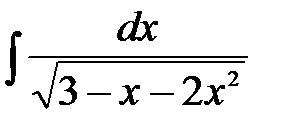Решение: Выделяя полный квадрат из квадратного трехчлена, имеем
.
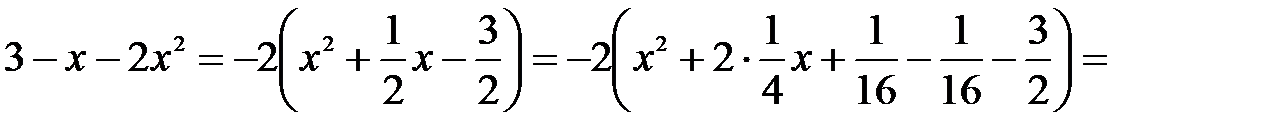
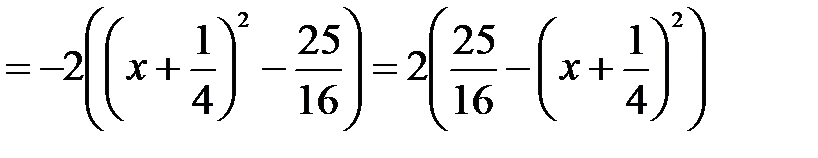Отсюда получаем
.
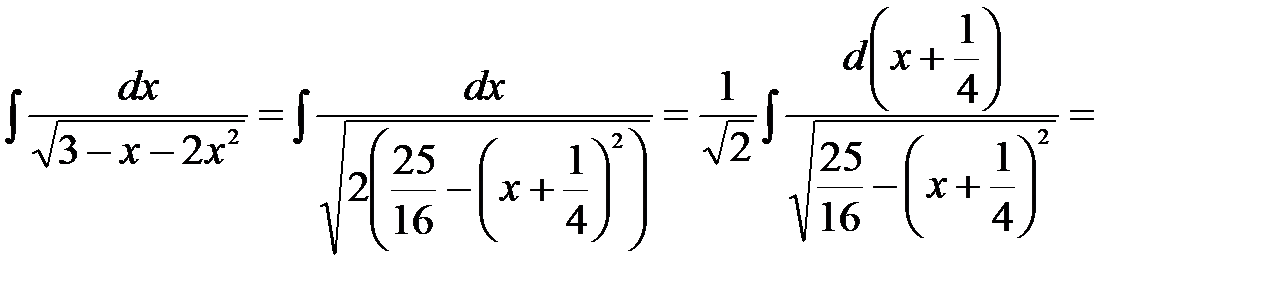
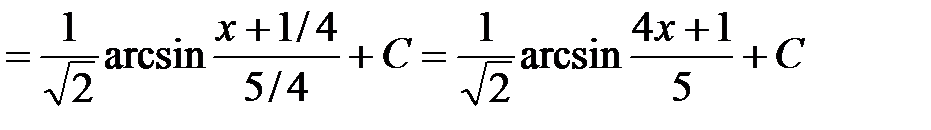4) 
.
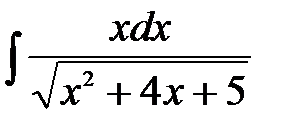Решение: Сначала выделим полный квадрат из квадратного трехчлена
.
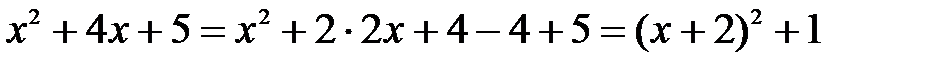Таким образом,
.
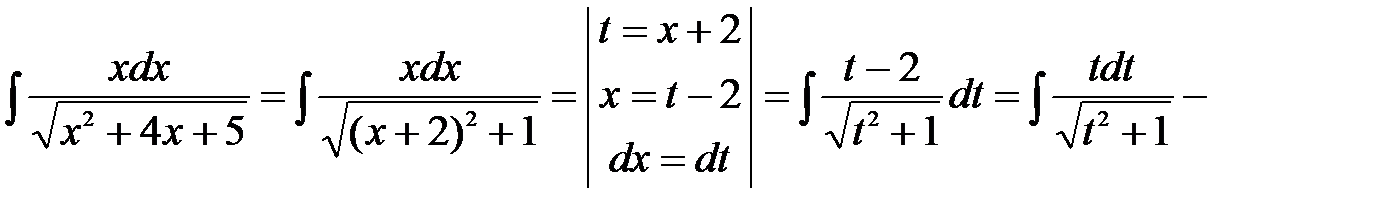
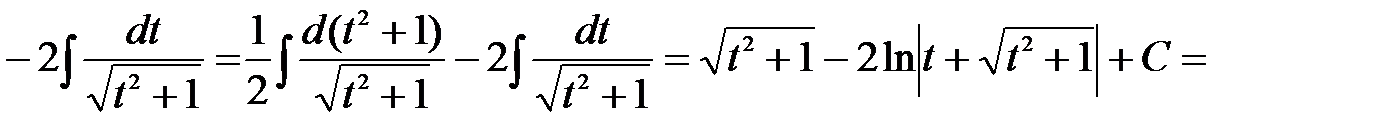
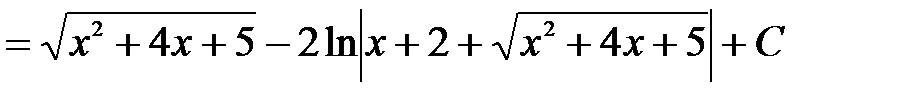Задания для самостоятельной работы по теме
«Интегрирование функций, сордержащих квадратный трехчлен».
Задание. Вычислить следующие интегралы:
16.1.  .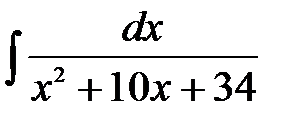
| 16.2.  .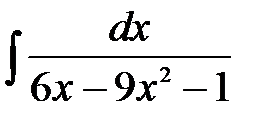
|
16.3.  .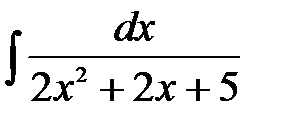
| 16.4.  .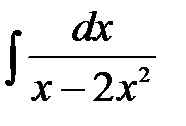
|
16.5.  .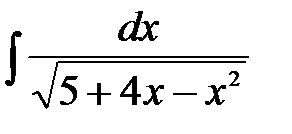
| 16.6.  .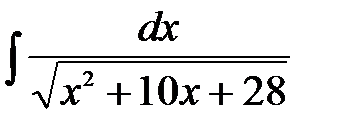
|
16.7.  .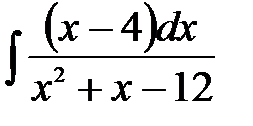
| 16.8.  .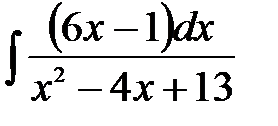
|
16.9.  .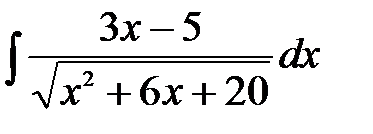
| 16.10.  .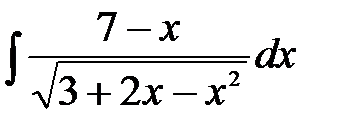
|
Тема17. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ДРОБЕЙ.
