Формула интегрирования по частям

Если и − дифференцируемые функции, то справедливо

.

Данная формула называется формулой интегрирования по частям. Она дает возможность свести вычисление интеграла 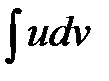к вычислению интеграла , который оказывается более простым.

При нахождении интегралов типа

, ,

за следует принять многочлен , а за 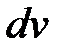− соответственно выражения , , ; при отыскании интегралов вида

, , ,

,

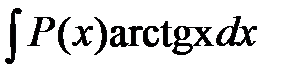за принимаются соответственно функции , , , , , а за − выражение .

Примеры 15. Вычислить интегралы:

1) .

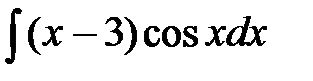Решение: Воспользуемся формулой интегрирования по частям:

.

2) .

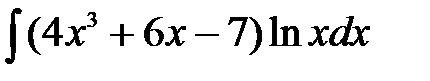Решение: Воспользуемся формулой интегрирования по частям:

.

3) .

Решение: Воспользуемся формулой интегрирования по частям:

.

4) .

Решение: Воспользуемся формулой интегрирования по частям, получим:

.

К последнему интегралу снова применим формулу интегрирования по частям:

.

Подставляя найденное выражение в первоначальное выражение, имеем

.

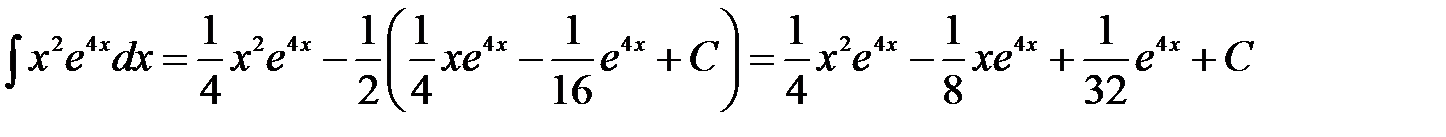5) .

Решение: Воспользуемся формулой интегрирования по частям:

.

Последний интеграл сновапроинтегрируем раз по частям:

.

Таким образом,

.

В правой части последнего соотношения стоит искомый интеграл . Перенося его в левую часть, получим

.

Откуда

.

Задания для самостоятельной работы по теме

«Интегрирование по частям».

Задание. Проинтегрировать по частям следующие интегралы:

15.1. .	15.2. .	15.3. .
15.4. .	15.5. .	15.6. .
15.7. .	15.8. .	15.9. .
15.10. .	15.11. .	15.12. .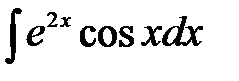
15.13. .	15.14. .	15.15.

Тема16. ИНТЕГРИРОВАНИЕ ФУНКЦИЙ, СОДЕРЖАЩИХ КВАДРАТНЫЙ ТРЕХЧЛЕН.