Интегрирование простейших дробей

Определение 17.1. Рациональная дробь , где − многочлены степени и соответственно, называется правильной, если . Если , то дробь называется неправильной.

Определение 17.2. Простейшими рациональными дробями называются дроби, относящиеся к следующим четырем типам:

I. .II. . III. . IV. .

Здесь – постоянные числа, , а – квадратный трехчлен, не имеющий действитель­ных корней.

Простейшие дроби интегрируются следующим образом:

,

.

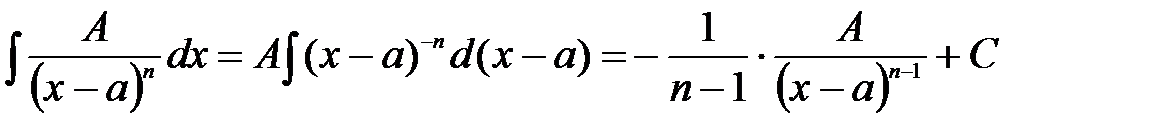Интегрирование простейшей дроби III типа было рассмотрено
в теме 16 «Интегрирование функций, содержащих квадратный трехчлен».

Для интегрирования простейшей дроби IV типа сначала следует выделить полный квадрат из квадратного трехчлена в знаменателе дроби, т.е. . Затем сделать подстановку и разложить полученный интеграл на сумму двух интегралов: первый интеграл интегрируется непосредственно, второй интеграл с помощью рекуррентной формулы:

.