Вектор – это направленный отрезок. Длина вектора называется его модулем. Если модуль равен нулю, то вектор – нулевой, он не имеет направления.
Коллинеарные векторы – векторы, лежащие на одной или параллельных прямых
Линейные операции.
1) сложение (правило треугольника, правило параллелограмма, вычитание вектора)
2) умножение вектора на число
Свойства линейных операций над векторами.
1) 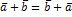 - переместительное свойство
- переместительное свойство
2) 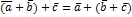 – сочетательное
– сочетательное
3) 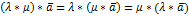
4) 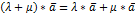 – распределительный закон
– распределительный закон
5) 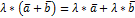 - распределительное свойство
- распределительное свойство
Линейная зависимость векторов. Базис
 – является линейной комбинацией векторов
– является линейной комбинацией векторов 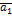 ,
, 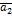 …
… 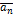 , если он может быть представлен в виде
, если он может быть представлен в виде 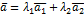 …+
…+ 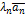 , где
, где 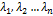 - некоторые числа. В этом случае говорят, что вектор
- некоторые числа. В этом случае говорят, что вектор  разложен по базису
разложен по базису 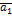 ,
, 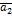 …
… 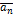
Любая пара неколлинеарных векторов в плоскости образует базис на плоскости.
Три вектора называются компланарными если они лежат в одной или параллельных плоскостях.
Любая тройка некомпланарных векторов образует базис в пространстве.
| l |
| A’B’ |
| A |
| B |
Проекцией вектора АВ на ось называется число равное длине A’B’ и взятое со знаком «+» если совпадает с направлением оси и со знаком «-» если в разных направлениях.
Проекция вектора на ось равна произведению модуля вектора на косинус угла между вектором и осью.
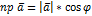
Следствие.
1) 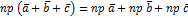
2) 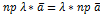
 2018-01-08
2018-01-08 360
360








